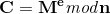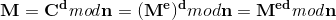历史发展自行百度!
首先看一下对于明文块M和密文块C,加密和解密使用的两个公式(形式):
在这里,发送者和接受者都必须知道n和e的值,而且只有接受者知道d的值(这就是接受者的私钥,私钥很重要)。所以,这种公钥加密算法的公钥KU={e, n}, 私钥 KR={d, n}。
网络安全有关加密这部分对数学的要求还是蛮高的,这里就简单的说一下公钥和密钥的生成过程,然后通过一个例子简单使用模拟一个解密的过程:
首先选择两个素数p和q,并且计算出它们的积n,这里的n就是加密和解密过程中会使用的模。
然后计算Φ(n),计算这个是为了计算后面的e,Φ(n)的计算是使用欧拉函数计算出了小于n并且与n互素的所有整数的数量,可以使用Φ(n)=(p - 1)(q - 1)来进行计算(这样看来欧拉公式和这个结果又有什么关系?我也不太懂,说了数学基础要有的,不过可以这样理解,计算n时是使用两个素数p、q的乘积计算的,现在要计算小于n并且与n互素的所有整数的数量,那么每次乘之前减去自身,也就是每次相乘都要减去1……算了挺乱的,就这样,直接看结果)。
计算完成之后,选择与Φ(n)互素并且小于Φ(n)的整数e(e和Φ(n)的最大公约数为1),这里是选择,毕竟结果不唯一,也保证了更加的安全。
最后再计算d,它是e关于modΦ(n)的乘法逆元(好吧,又有数学概念了,其实就是计算de mod Φ(n) = 1, 并且d小于Φ(n))。好了,如下例生成一个密钥:
- 选择两个素数p = 17 和 q = 11.
- 计算n = pq = 17×11 = 187.
- 计算Φ(n) = (p - 1)(q - 1) = 16 × 10 = 160.
- 选择与Φ(n) = 160 互素的数,并且小于Φ(n)的e,我们选择得到e = 7.
- 确定d满足de mod 160 = 1, 并且d < 160. 得到d = 23.
这个计算的过程并非可以通过公式一次性计算出来,所以慢慢蒙吧……
计算完成得到n = 187, Φ(n) = 160, e = 7, d = 23
最终确定密钥为: 公钥KU = {7, 187}, 私钥KR = {23, 187}。
然后我们通过这组密钥来对输入明文M = 88进行加密:
我们使用如下公式加密计算:
得到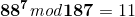
然后使用如下公式解密计算:
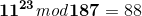
就是如上的一个过程,从产生密钥到对一个数据的加密以及解密的过程,然后我们来看一个题目应用一下:
在使用RSA的公钥系统中,你窃听到发送密钥为e = 5, n = 35的用户密文C = 10.对应的明文是什么?
首先我们明确几个值:
- e = 5, 发送者使用的公钥
- n = 35,加密和解密使用的模
- C = 10,密文
对于这样一个问题我们使用公式必须要知道d的值才能进行解密运算,我们可能要从密钥产生的步骤来出发了.
我们先确定两个素数p 和 q 的值, p和q为两个素数,乘积结果为n,得到 p = 5, q = 7. (p, q 值的得到是一个不可逆推的过程,所以当n值较大的时候,破解也是非常困难的)。
然后我们通过p、q的值计算Φ(n) = (p - 1)(q - 1) = 24, 题目告知e = 5,所以就可以计算d了:
de mod Φ(n) = 1 ====》d * 5 mod 25 = 1 ,得到的d = 5
最后通过公式进行解密:
M = 10^5 mod 35 得到明文为:5
通过上述的过程我们会发现,RSA加密算法破解的过程并非是公式化的,因为它使用的公式往往是不可逆推的,我们需要去进行尝试,当数据较小时我们很容易破解,但是当数据值增大时,我们会很明显的发现计算出现了一定的难度,可以说有时候还需要一定的运气。
RSA有两个密钥,分别是公钥和私钥,公钥可以公开出去,加密之后通过私钥来进行解密,私钥必须自己掌握,否则就等同与信息泄露了。
!!!学习过程的简单总结,不足之处还望指教!!!