前言
断断续续学遗传到现在快一个礼拜了,之前一直在看思想,死想活想,始终不敢去自己代码实现。
今天硬着头皮开始写,写不下去就找博文看,总算是初步的实现了,迈出了智能算法学习的第一小步,心情不可谓不激动。
好吧,说正经的。
tsp&旅行商问题
旅行商问题,即TSP问题(Traveling Salesman Problem)是数学领域中著名问题之一。
假设有一个旅行商人要拜访N个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。
路径的选择目标是要求得的路径路程为所有路径之中的最小值。
遗传算法
算法思想
从遗传两个字,不难想到,这个算法是由生物进化的机理所抽象出来的一种思想。
对于一个问题,有许多可能的解。
就拿上述的tsp问题来说吧,每一种遍历顺序都是一个解。所有城市顺序的全排列合在一起就是这个问题的解集。
我们将每个解都看做一个个体。那么多个个体放在一起就可以构成一个种群。
大自然每个种群都要经过漫长的自然选择,也就是优胜劣汰,以及繁殖和变异。
而解所构成的种群也不例外。
显然,我们可以很明确的对每个个体的优劣性进行评价。本体的条件是总路程最短,根据解得到总路程的大小是很容易的。
评价过后,对于每个个体的优劣我们都已掌握。
那么残酷的地方来了,我们要杀死(淘汰)一部分个体。
当然也不能光杀,温馨的部分也是有的,那就是两两个体交叉繁殖,产生后代。
除此之外,还要有一点幸运度,那就是变异了,随机的对某些个体进行一些改变。
上述操作进行完之后,我们已经相当于更新了整个群体。
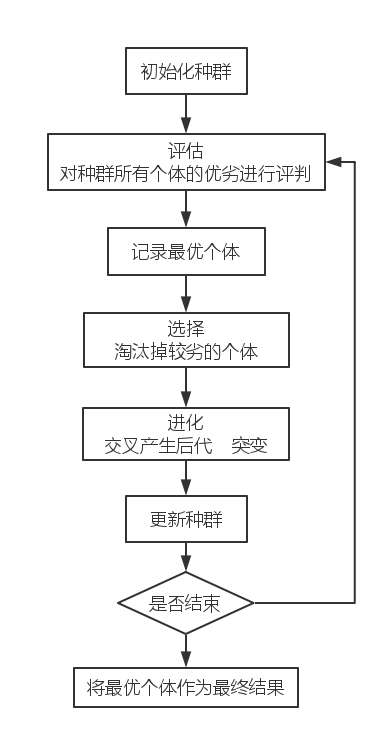
然后重复的进行此过程,直到得到满意的(个体)结果。
上述内容总结一下,就是下图。
交叉方式与变异方式
交叉方式有很多种,对于不同的问题,交叉方式的不同对于求解会有一定的影响。
变异同理。
这里只介绍我所用的方式。其实也是最普通最常用的方式。
交叉方式
父个体:1 2 3 4 9 8 7 6 5 0
母个体:7 8 9 0 1 6 5 4 3 2
那么随机取两个值,比如:4和6
将父个体划分:1 2 3 [4 9] 8 7 6 5 0
则,将划分区间内的基因赋给子个体
子个体:x x x 4 9 x x x x x
再按照母个体的基因顺序赋值给子个体
子个体:7 8 0 4 9 1 6 5 3 2
变异方式
个体: 1 2 3 4 9 8 7 6 5 0
还是随机选取两个值,比如:4和6
那么,交换位置4和位置6的基因。
新个体:1 2 3 8 9 4 7 6 5 0
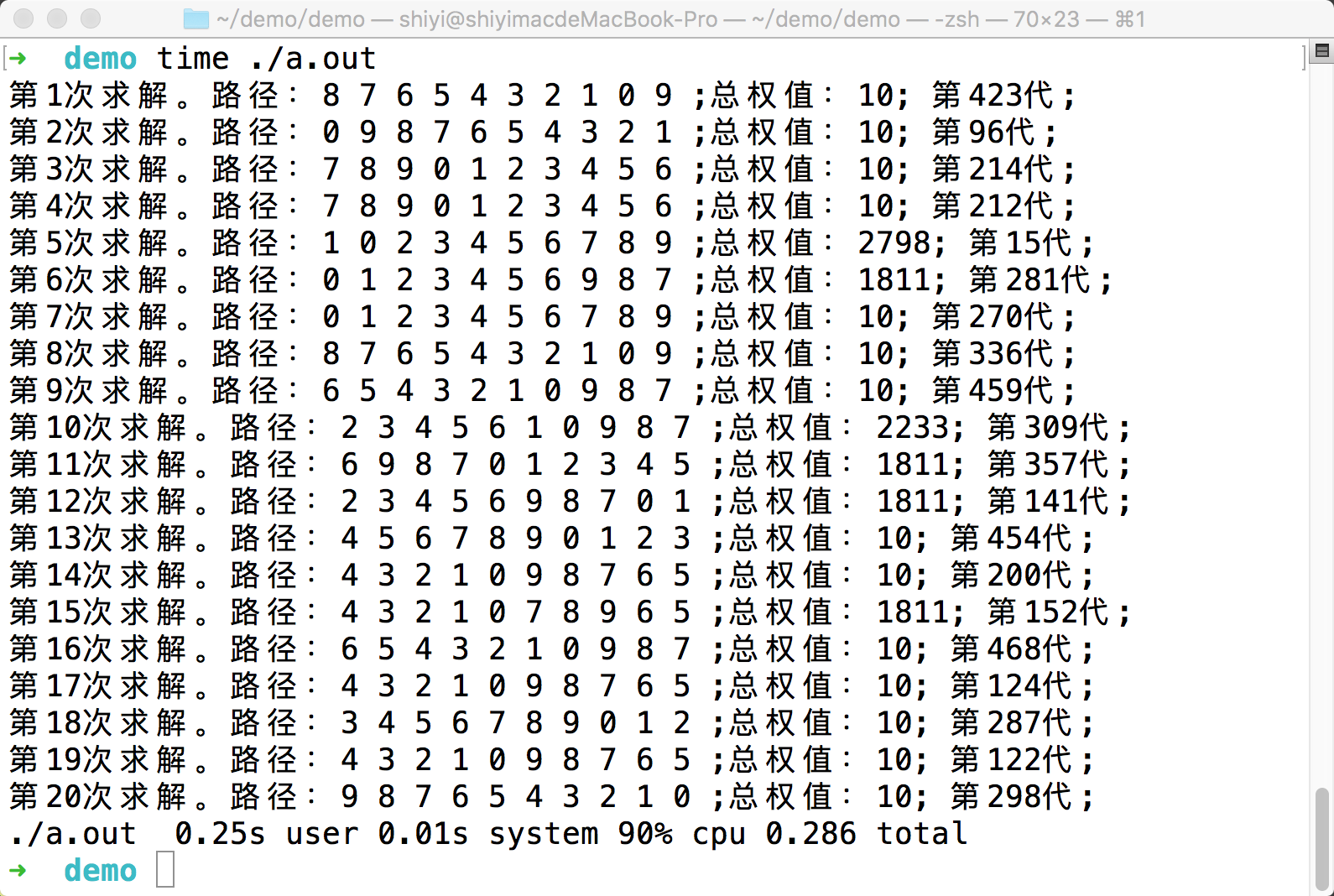
程序效果
可以看到,20次求解有14次得到了最优解,在牺牲了一定最优性的情况下,换取了程序快速得解的能力。
不足
因为是第一次写,交叉和变异都用了最常用也是最简单的方式。
对于同一个问题,使用不同的交叉方式和变异方式,效果会有很大不同。还有种群个体数量以及进化迭代次数,变异概率等等参数的不同取值,都会有影响。
而这些只有不停的实践,才可以真正掌握一定经验。长路漫漫,吾往矣!
代码
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
using namespace std;
const int city_num = 10;//城市数量
const int unit_num = 100;//群体规模
int ps = 10;//变异概率
const int genmax = 500;//最大迭代数
//城市间距离映射 最优解权值=10
int length_table[10][10] = {
{0,1,1272,2567,1653,2097,1425,1177,3947,1},
{1,0,1,2511,1633,2077,1369,1157,3961,1518},
{1272,1,0,1,380,1490,821,856,3660,385},
{2567,2511,1,0,1,2335,1562,2165,3995,933},
{1653,1633,380,1,0,1,1041,1135,3870,456},
{2097,2077,1490,2335,1,0,1,920,2170,1920},
{1425,1369,821,1562,1041,1,0,1,4290,626},
{1177,1157,856,2165,1135,920,1,0,1,1290},
{3947,3961,3660,3995,3870,2170,4290,1,0,1},
{1,1518,385,993,456,1920,626,1290,1,0}
};
class Unit
{
public:
int path[city_num];//个体的路径信息
int length;//个体价值
};
class Group
{
public:
Unit group[unit_num];
Unit best;
int best_gen;
Group()
{
best.length = 0x3f3f3f3f;
best_gen = 0;
for(int i = 0; i < unit_num; i++)
{
bool flag[city_num] = {};
for(int j = 0; j < city_num; j++)
{
int t_city = rand()%city_num;
while(flag[t_city])
t_city = rand()%city_num;
flag[t_city] = true;
group[i].path[j] = t_city;
}
}
}
//对每个个体进行评估
void assess()
{
for(int k = 0; k < unit_num; k++)
{
int rel = 0;
for(int i = 1; i < city_num; i++)
rel += length_table[group[k].path[i-1]][group[k].path[i]];
rel += length_table[group[k].path[city_num-1]][group[k].path[0]];
group[k].length = rel;
}
}
//根据评估结果对个体进行排序
void unit_sort()
{
for(int i = 0; i < unit_num; i++)
{
for(int j = i+1; j < unit_num; j++)
{
if(group[i].length > group[j].length)
{
Unit temp;
memcpy(&temp, &group[i], sizeof(Unit));
memcpy(&group[i], &group[j], sizeof(Unit));
memcpy(&group[j], &temp, sizeof(Unit));
}
}
}
}
//交叉
Unit cross(Unit &father, Unit &mother)
{
int l = rand()%city_num;
int r = rand()%city_num;
if(l > r)
swap(l, r);
bool flag[city_num] = {};
for(int i = l; i <= r; i++)
flag[father.path[i]] = true;
Unit son;
int pos = 0;
for(int i = 0; i < l; i++)
{
while(flag[mother.path[pos]])
pos++;
son.path[i] = mother.path[pos++];
}
for(int i = l; i <= r; i++)
son.path[i] = father.path[i];
for(int i = r+1; i < city_num; i++)
{
while(flag[mother.path[pos]])
pos++;
son.path[i] = mother.path[pos++];
}
return son;
}
//突变
void mutation(Unit &t)
{
int proport = rand() % 100;
if(proport > ps)
return;
int one = rand()%city_num;
int two = rand()%city_num;
while(two != one)
two = rand()%city_num;
swap(t.path[one], t.path[two]);
}
//输出信息
void print()
{
for(int i = 0; i < unit_num; i++)
{
printf("第%d个个体,路径信息:", i);
for(int j = 0; j < city_num; j++)
printf("%d ", group[i].path[j]);
printf(";总权值:%d;\n", group[i].length);
}
printf("最优个体,路径信息:");
for(int j = 0; j < city_num; j++)
printf("%d ", group[0].path[j]);
printf(";总权值:%d;\n", group[0].length);
}
//种群进化
void work()
{
for(int i = 0; i < genmax; i++)
{
//如果进化层数大于20,加大变异的概率
if(i > 20)
ps *= 3;
assess();//评估
unit_sort();//根据评估结果排序
if(best.length > group[0].length)
{
memcpy(&best, &group[0], sizeof(group[0]));
best_gen = i;
}
for(int j = 0; j+2 < unit_num; j+=3)
group[j+2] = cross(group[j], group[j+1]);
for(int j = 0; j < city_num; j++)//变异(从1开始,保留最优)
mutation(group[j]);
}
}
};
Unit group[unit_num];//种群变量
Unit bestone;//记录最短路径
int generation_num;//记录当前达到了第几代
int main()
{
srand((int)time(0));
for(int i = 0; i < 20; i++)
{
Group g;
g.work();
printf("第%d次求解。路径:", i+1);
for(int j = 0; j < city_num; j++)
printf("%d ", g.best.path[j]);
printf(";总权值:%d; 第%d代;\n", g.best.length, g.best_gen);
}
return 0;
}