| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 4839 | Accepted: 2032 |
Description
Polygon is a game for one player that starts on a polygon with N vertices, like the one in Figure 1, where N=4. Each vertex is labelled with an integer and each edge is labelled with either the symbol + (addition) or the symbol * (product). The edges are numbered from 1 to N.
On the first move, one of the edges is removed. Subsequent moves involve the following steps:
�pick an edge E and the two vertices V1 and V2 that are linked by E; and
�replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2.
The game ends when there are no more edges, and its score is the label of the single vertex remaining.
Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.
Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score.
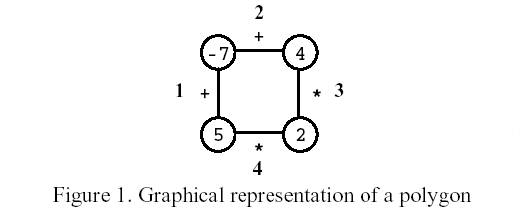
On the first move, one of the edges is removed. Subsequent moves involve the following steps:
�pick an edge E and the two vertices V1 and V2 that are linked by E; and
�replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2.
The game ends when there are no more edges, and its score is the label of the single vertex remaining.
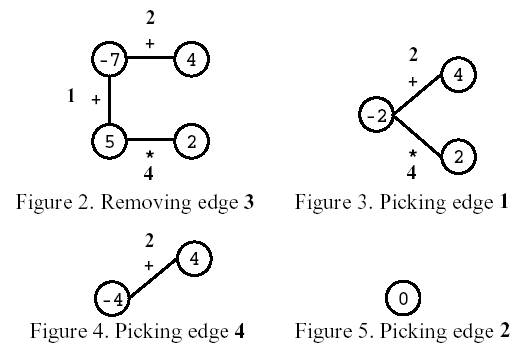
Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.
Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score.
Input
Your program is to read from standard input. The input describes a polygon with N vertices. It contains two lines. On the first line is the number N. The second line contains the labels of edges 1, ..., N, interleaved with the vertices' labels (first that of the vertex between edges 1 and 2, then that of the vertex between edges 2 and 3, and so on, until that of the vertex between edges N and 1), all separated by one space. An edge label is either the letter t (representing +) or the letter x (representing *).
3 <= N <= 50
For any sequence of moves, vertex labels are in the range [-32768,32767].
3 <= N <= 50
For any sequence of moves, vertex labels are in the range [-32768,32767].
Output
Your program is to write to standard output. On the first line your program must write the highest score one can get for the input polygon. On the second line it must write the list of all edges that, if removed on the first move, can lead to a game with that score. Edges must be written in increasing order, separated by one space.
Sample Input
4 t -7 t 4 x 2 x 5
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 4839 | Accepted: 2032 |
Description
Polygon is a game for one player that starts on a polygon with N vertices, like the one in Figure 1, where N=4. Each vertex is labelled with an integer and each edge is labelled with either the symbol + (addition) or the symbol * (product). The edges are numbered from 1 to N.
On the first move, one of the edges is removed. Subsequent moves involve the following steps:
�pick an edge E and the two vertices V1 and V2 that are linked by E; and
�replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2.
The game ends when there are no more edges, and its score is the label of the single vertex remaining.
Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.
Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score.
On the first move, one of the edges is removed. Subsequent moves involve the following steps:
�pick an edge E and the two vertices V1 and V2 that are linked by E; and
�replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2.
The game ends when there are no more edges, and its score is the label of the single vertex remaining.
Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.
Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score.
Input
Your program is to read from standard input. The input describes a polygon with N vertices. It contains two lines. On the first line is the number N. The second line contains the labels of edges 1, ..., N, interleaved with the vertices' labels (first that of the vertex between edges 1 and 2, then that of the vertex between edges 2 and 3, and so on, until that of the vertex between edges N and 1), all separated by one space. An edge label is either the letter t (representing +) or the letter x (representing *).
3 <= N <= 50
For any sequence of moves, vertex labels are in the range [-32768,32767].
3 <= N <= 50
For any sequence of moves, vertex labels are in the range [-32768,32767].
Output
Your program is to write to standard output. On the first line your program must write the highest score one can get for the input polygon. On the second line it must write the list of all edges that, if removed on the first move, can lead to a game with that score. Edges must be written in increasing order, separated by one space.
Sample Input
4 t -7 t 4 x 2 x 5
Sample Output
33 1 2题目大意:
给定一个由n（3<=n<=50）的顶点围成的一个多边形，且每一条边上存在一个,符号t(+),x(*)，现在需要先从某处将该图形剪开,使之成为一个链，然后如果现在定点数大于以（相当于链长大于一），可以任选一点与其左边或者右边的点通过相连的边来进行计算得到新的顶点将原来的的顶点代替.继续该操作.
要求找到可能得到最大的结果（最后链长为一时只剩下一个顶点）.
我的想法.如果从第i个运算符前截断，现在把后面n-i+1个数及其运算符号放在前面.讲i-1个运算符放在后面.现在就相当于是求一个表达式的值带括号的表达式的值.(括号可以改变+ * 的顺序).
记dp[i][j]为从第i个数计算道第j个数的最大结果.
讲n个数存放道a[1]...a[n]之中.
第i个数于第i+1个数存放于p[i+1]之中,p[1]存放的是a[1]于a[n]的运算
如果p[k+1]=='t'是?是+，否则是*
dp[i][j]=max(dp[i][j],dp[i][k] ? dp[k+1][j]);
第一步的切断位置是通过枚举得来的.
写好提交错误，很不解.在discuss中找了数据发现有负数的时候就会出错。想明白了求实两个绝对值之积大于有可能大于两个整数的积.
现在有a，b<0 0<x，y
现在求他们两数运算的最大结果.ans
若是加法.
如果运算符是加
ans=max(a+b)
是乘法的时候
ans=max(a*b,x*y).
现在增加状态.
dpmin[i][j]为从第i个数道第j个数的运算最小结果.
然后跟新状态详见代码.(由于手残把 左移 写成了 < 最大值，与最小值都没有设置好，检查了半天，埃)
具体如下.
/* Source Code
Problem: 1179 User:
Memory: 760K Time: 32MS
Language: G++ Result: Accepted
Source Code*/
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define MAX ((1 << 30 ) -1)
#define MIN (- MAX)
#define maxn 80
char ptt[maxn]={0};
char p[maxn]={0};
int a[maxn]={0};
int att[maxn]={0};
int ans[maxn]={0};
int dp[maxn][maxn];
int dpmin[maxn][maxn];
int path[maxn][maxn];
int getNo(int no,int k,int n){
if(no>=k) no=no-(k-1);
else no=no+(n-k+1);
}
int slove(int n){
int i,j,k,pos;
char ptemp[maxn];
char atemp[maxn];
for(pos=1;pos<=n;pos++){
//memset(path,-1,sizeof(path));
for(i=1;i<pos;i++){
ptemp[i+n-pos+1]=ptt[i];
atemp[i+n-pos+1]=att[i];
}
for(i=pos;i<=n;i++){
ptemp[i-pos+1]=ptt[i];
atemp[i-pos+1]=att[i];
}
for(i=1;i<=n;i++){
a[i]=atemp[i];
p[i]=ptemp[i];
// cout<<p[i]<<' '<<a[i]<<' ';
}
//cout<<endl;
for(i=1;i<=n;i++){
dp[i][i]=a[i];
dpmin[i][i]=a[i];
}
for(k=1;k<=n;k++){
for(i=1;i+k<=n;i++){
dp[i][i+k]=MIN;
dpmin[i][i+k]=MAX;
for(j=i;j<i+k;j++){
if(p[j+1]=='t'){
dp[i][i+k]=max(dp[i][j]+dp[j+1][i+k],dp[i][i+k]);
dpmin[i][i+k]=min(dpmin[i][i+k],dpmin[i][j]+dpmin[j+1][i+k]);
}
if(p[j+1]=='x'){
dp[i][i+k]=max(dp[i][j]*dp[j+1][i+k],dp[i][i+k]);//1,1
dp[i][i+k]=max(dpmin[i][j]*dpmin[j+1][i+k],dp[i][i+k]);//0,0
dp[i][i+k]=max(dp[i][j]*dpmin[j+1][i+k],dp[i][i+k]);//1,0
dp[i][i+k]=max(dpmin[i][j]*dp[j+1][i+k],dp[i][i+k]);//0,1
dpmin[i][i+k]=min(dpmin[i][i+k],dpmin[i][j]*dpmin[j+1][i+k]);//0,0
dpmin[i][i+k]=min(dpmin[i][i+k],dp[i][j]*dp[j+1][i+k]); //1,1
dpmin[i][i+k]=min(dpmin[i][i+k],dp[i][j]*dpmin[j+1][i+k]); //1,0
dpmin[i][i+k]=min(dpmin[i][i+k],dpmin[i][j]*dp[j+1][i+k]); //0,1
}
}
}
}
ans[pos]=max(dp[1][n],dpmin[1][n]);
//cout<<"cut: "<<pos<<" ans: "<<ans[pos]<<" dp[1][n]: "<<dp[1][n]<<" dpmin[1][n] "<<dp[1][n]<<endl;
}
}
int main(){
int n,i;
while(scanf("%d",&n)!=EOF){
for(i=1;i<=n;i++){
cin>>ptt[i];
cin>>att[i];
//cout<<pt[i]<<' '<<at[i]<<' ';
}
slove(n);
int __min=MIN;
for(i=1;i<=n;i++){
__min=max(__min,ans[i]);
}
cout<<__min<<endl;
for(i=1;i<=n;i++){
if(ans[i]==__min)
cout<<i<<' ';
}
cout<<endl;
}
return 0;
}