- 在257瓶水中有1瓶有毒,毒发时间为2小时,在两小时中要用多少只小白鼠才能找出有毒的水。
解答: 9只 , 9个二进制位可以代表 512 个数 。给每瓶水编号,让9只小白鼠代表9个二进制位,若二进制位为 1 则喝该编号的水,0 则不喝 。
- 25匹马,5条赛道,一匹马一个赛道,比赛只能得到5匹马之间的快慢程度,而不是速度,求决胜1,2,3名至少多少场。
A. 6 B. 7 C. 8 D. 12
解答:
7场。
5场比赛定出每组最快的马,1场比赛定出每组的名次,本场比赛可定出第一名以及淘汰两组马,分别用第一名的组的2,3名和第2名的组的1,2名和第3名组的1名进行1场比赛,定出2,3名,至此比赛完毕。
- 小组赛,每个小组有5支队伍,互相之间打单循环赛,胜一场3分,平一场1分,输一场不得分,小组前三名出线。平分抽签。问一个队最少拿( )分就有理论上的出线希望()
A.1 B.2 C.3 D.4
解答:
前两名分别取得4胜和3胜,后三名之间都是平局,后三名积分都为2,抽签决定出线。
- 在一冒险游戏里,你见到一个宝箱,身上有N把钥匙,其中一把可以打开宝箱,假如没有任何提示,随机尝试,问:
(1)恰好第K次(1<=K<=N)打开宝箱的概率是多少。
(2)平均需要尝试多少次。
解答:
1.1 / N
2. 列出分布律,求出数学期望。(N+1)/ 2
等差数列求和公式:
Sn=n*a1+n(n-1)d/2或Sn=n(a1+an)/2
等比数列求和公式:
推广式:
Sn=n*a1 (q=1)
Sn=a1(1-q^n)/(1-q) = (a1-an*q)/(1-q) (q≠1)
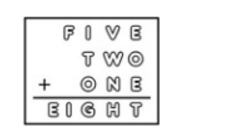
- 下图是一个英文等式。每个英文字母代表0~9中的一个数字。现已知:V=2,W=4,N=7。
F代表( )
A.2 B.4 C.7 D.9
解答:F只能向前进1位,E为1,I+T+O最多27,所以F为8或9,选D。
较真同学的推导:
9021+846+671=10538
所E=1 O=6 I=0 T=8 F=9
第一步,先得出E=1
理由,4位数和2个3位数的和是5位数,9999+999+999<20000,所以,一定是10000多
第二步,看千位和百位上
F如果是8,那么必须进2位,由于不可能进3位,所以,I=0,再看百位,有个I,所以不可能进2位,所以只能进1位,所以F是9,同时,I是0
第三步,看个位上
E+E+O=T,就是2+O=T
0,1,2,4,7,9已经用过了,所以只有3,5和6,8
所以个位是没有进位的,所以十位上H是3,于是个位上O是6,T是8
最后一步,G是5
- 给你8颗小石头和一架天平。其中7颗石头重量是一样的,另外一个比这7颗略重。请问在最坏的情况下,最少要称量几次,才能把这颗最终的石头找出来?
解答:4 VS 4 称一次 , 重的那边 2 VS 2 称一次 ,重的那边 1 VS 1 称一次 ,共3次 。
- 小松鼠采到了100 颗坚果要运回家。家离放坚果的地方有100 米远。小松鼠每次最多运 50 颗。BUT!小松鼠很馋。。。每走2 米就要吃一颗坚果。。。问小松鼠最多能运回家多少颗坚果?
A. 0 B.10 C.25 D.50
解答:C
设采坚果的地点为A,家为B,从A到B方向的运动需要消耗坚果。题目求最多运多少坚果回家,为使结果最大化,所以需要每次开始都运50颗,所以题目也就是求最少的坚果消耗量,由于A->B方向的运动一直要消耗坚果,所以也就是求此方向运动的最少距离。由于每次做多运50颗,所以有一段A->B方向必须走两次,设这段距离为x,剩下的距离为y,则有x+y=100。消耗的总坚果数为(2x+y)/2。并且为了使最后y段能够运走所有2x段剩下的坚果,需要满足2*(50-x/2)<=50,所以x>=50。由于要使(2x+y)/2=(x+100)/2最小,所以x应该去最小值50,所以消耗坚果数为(50+100)/2=75,所以剩下25个
?处的图形是( A )
解答:中心连接的2根火柴每次顺时针转动45度。
- 一群朋友聚餐。上第一瓶酒的时候,各人平分。一瓶喝下来,有几个朋友有急事就离开了。第二瓶酒上来的时候,余下的人平分,喝完的时候有几个人也有事情离开了。上第三瓶酒的时候还是余下的人平分。喝完的时候其中一个人道:“嘿,我正好喝了一瓶”。请问一共有几个人聚在一起喝酒?
解答:
总共三瓶酒,其中一人喝了三次,如果每次喝1/3是可以喝完的,但人数在发生变化,所以,必然有一次喝酒的量大于1/3瓶;由于是平均分,所以分子是1分母是整数,所以,最后一次就是2人对垒,而且三次的人数都不相等,所以不能是1/2+1/4+1/4=1,所以,只能是一个大于1/4,一个小于1/4的,所以,只有1/2+1/3+1/6满足条件,因此最初的人是6人
- 两人玩游戏,在脑门上贴数字(正整数>=1),只看见对方的,看不见自己的,而且两人的数字相差1,以下是两人的对话: A:我不知道 B:我也不知道 A:我知道了 B:我也知道了 问A头上的字是多少,B头上的字是多少( )
A是4,B是3
A是3,B是2
.A是2,B是1
A是1,B是2
解答:B
1. A看到B为2,不确定A为1或3;所以不知道;
2 B看到A为3,不确定B为2或4;所以也不知道;
3 A听到B说B也不知道,排除了A为1;所以A为3;
4 B听到A说A知道了,排除了B为4;所以B为2
- 有一种体育竞赛共含M个项目,有运动员A,B,C三人参加,在每一项目中,第一,第二,第三名分别得X,Y,Z分,其中X,Y,Z为正整数且X>Y>Z。最后A得22分,B与C均得9分,B在百米赛中取得第一。求M的值及在跳高中谁得第二名。
A. 5 ,A B. 5,C C. 4,B D. 4,A
解答:
首先计算M个项目的总分:22+9+9=40分;
1.若分4个项目,则每个项目的分数为:X+Y+Z=10分,由X>Y>Z关系可得以下3种分配:
①X=7,Y=2,Z=1;
②X=5,Y=4,Z=1;
③X=5,Y=3,Z=2。
然后,A总分22,按②和③分配的话,取最高分5分来计算,即便是A在这4个项目中都拿第一也只有20分,故只能是①的分配。还是从A入手,22分可以由3次第一(即X=7分)和1次第三(即Z=1分)组成,因为只有4个项目,所以A拿第三的一定在百米项目中,这样百米的排名是:B>C>A。接着,在剩下的3个项目中,A都是第一,第二可能是B或者C,拿B来说,B的总分9分可以由1次第一(百米项目,X=7分)和1次第二(Y=2分)组成,剩下的位置全由C填补,这样明显违背了排名原则,因为会出现2次A>C>C的奇怪逻辑。
同样,拿C来说,即是C的总分9分可以由4次第二(Y=2分)和1次第三(Z=1分)组成,然后剩余的位置由C填补,同样出现了上述A>C>C的奇怪逻辑,故4个项目不符合题意。
2.分5个项目,则每个项目的分数为:X+Y+Z=8分,同理有以下2种分配:
①X=5,Y=2,Z=1;
②X=4,Y=3,Z=1。
然后,A总分22,按②分配的话,取最高分4分计算,假设5个项目A都第一,也只有20分,故排除。这样就是①的分配原则。计算下来,便可知跳高中C拿第二。故选项B正确。
- 有一个大西瓜,用水果刀平整地切,总共切9刀,最多能切成多少份,最少能切成多少份?
解答:
最少为0,最多为130
将n从0到9依次列出,发现红色部分的数值均为其左边与左上角的两个数之和。
n 0 1 2 3 4 5 6 7 8 9
n个点最多能把直线分成多少部分 1 2 3 4 5 6 7 8 9 10
n条直线最多能把平面分成多少部分 1 2 4 7 11 16 22 29 37 46
n个平面最多能把空间分成多少部分 1 2 4 8 15 26 42 64 93 130
链接
- 两根绳子,燃烧时间均为1个小时(燃烧速度不均匀),现给你一个打火机,如何准确度量45分钟时间?
解答:
1、将第一根从两头开始双向同时烧,与此同时,将第二根绳子从一头开始单向烧。
2、第一根绳子烧完之后,是半个小时;与此同时,第二根绳子也刚好烧完一般,再将第二根绳子的另一头点燃,可以刚好用15分钟烧完。
3、累加下来,刚好是45分钟。