什么是范数?
范数,是具有“长度”概念的函数。在线性代数、泛函分析及相关的数学领域,范数是一个函数,是矢量空间内的所有矢量赋予非零的正长度或大小。
在数学上,范数包括向量范数和矩阵范数。
向量范数表征向量空间中向量的大小,矩阵范数表征矩阵引起变化的大小。 一种非严密的解释就是,对应向量范数,向量空间中的向量都是有大小的,这个大小如何度量,就是用范数来度量的,不同的范数都可以来度量这个大小,就好比米和尺都可以来度量远近一样;对于矩阵范数,学过线性代数,我们知道,通过运算AX=B,可以将向量X变化为B,矩阵范数就是来度量这个变化大小的。
为什么要引入范数?
我们都知道,函数与几何图形往往是有对应的关系,这个很好想象,特别是在三维以下的空间内,函数是几何图像的数学概括,而几何图像是函数的高度形象化。
但当函数与几何超出三维空间时,就难以获得较好的想象,于是就有了映射的概念,进而引入范数的概念。
当我们有了范数的概念的后,我们就可以引出两个向量的距离的定义,这个向量可以是任意维数的。通过距离的定义,进而我们可以讨论逼近程度,从而讨论收敛性、求极限。
向量的范数
定义
在数学上,对于向量范数的定义,就是只要满足以下三条性质的函数,我们就可以称为它为范数。

所以,范数的是一个宽泛的概念,有很多种,但是我们一般只会用到常用的范数,接下来我们介绍常用的向量范数。
常用向量函数
L0范数:
定义为
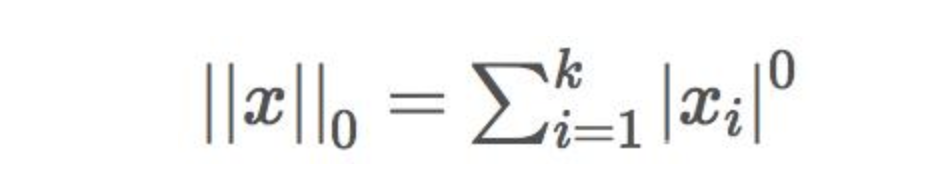
即非0元素个数。
L0范数表示向量中非零元素的个数。L0范数的这个属性,使其非常适用于机器学习中的稀疏编码。在特征选择中,通过最小化L0范数来寻找最少最优的稀疏特征项。但是,L0范数的最小化问题是NP难问题。而L1范数是L0范数的最优凸近似,它比L0范数要更容易求解。因此,优化过程将会被转换为更高维的范数(例如L1范数)问题。
L1范数:
定义为

L1范数是向量中各个元素绝对值之和,也被称作“Lasso regularization”(稀疏规则算子)。
L2范数:
定义为

L2范数是最常用的范数了,我们用的最多的度量距离欧氏距离就是一种L2范数。在回归里面,有人把加了L2范数项的回归c称为“岭回归”(Ridge Regression),有人也叫它“权值衰减weight decay”。它被广泛的应用在解决机器学习里面的过拟问题合。
为什么L2范数可以防止过拟合?回答这个问题之前,我们得先看看L2范数实际上是什么。
L2范数是指向量各元素的平方和然后求平方根。我们让L2范数的规则项最小,可以使得的每个元素都很小,都接近于0,但与L1范数不同,它不会让它等于0,而是接近于0,这是有很大的区别的。而越小的参数说明模型越简单,越简单的模型则越不容易产生过拟合现象。为什么越小的参数说明模型越简单?因为当限制了参数很小,实际上就限制了多项式某些分量的影响很小,这样就相当于减少参数个数。
Lp范数:
定义为

其实,L0、L1、L2都是Lp范数的特例,分别对应P=0、1、2的情况。
无穷范数:
定义为
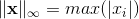
它主要被用来度量向量元素的最大值
PS
L2范数其实就是向量的标准内积,向量的长度一定是范数,长度是范数的充分条件,但不是必要条件,也就是说,范数不一定就是向量的长度。由长度定义的性质可知,满足长度的定义要符合平行四边形。举一个反例就可以证明非必要性:向量L1范数不满足平行四边形法则(A=(0,1)、B=(1,0))。
由内积决定的长度具有更丰富的几何结构。
矩阵的范数
跟向量的范数定义类似,只不过矩阵的范数的性质比向量的范数性质多了一条相容性。
我们直接引出矩阵的范数定义:
定义

矩阵范数的第三条性质也称为加法相容性,第四条是乘法相容性,前提都是矩阵之间可以进行加法或乘法的运算。
常用矩阵范数
1-范数:
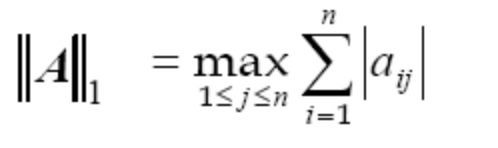
A的每列元素绝对值之和的最大值,也称为A的列范数。
无穷-范数:
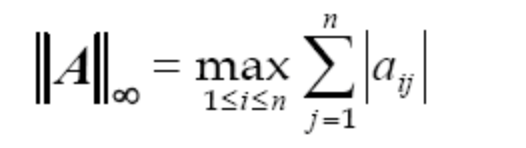
A的每行元素绝对值之和的最大值,也称为A的行范数。
2-范数:
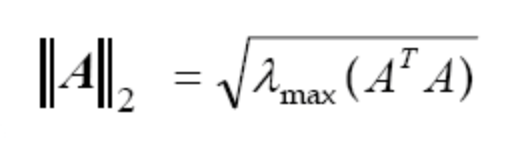
谱范数,即ATA矩阵的最大特征值的开平方。
PS
计算机领域用的比较多的就是迭代过程中收敛性质的判断,一般迭代前后步骤的差值的范数表示其大小,常用的是二范数,差值越小表示越逼近实际值,可以认为达到要求的精度,收敛。
总的来说,范数存在的意义是为了实现比较距离。比如,在一维实数集合中,我们随便取两个点4和9,我们知道9比4大,但是到了二维实数空间中,取两个点(1,0)和(3,4),这个时候我们就没办法比较它们之间的大小,因为它们不是可以比较的实数,于是我们引入范数这个概念,把我们的(1,0)和(3,4)通过范数分别映射到实数1 和 5 ,这样我们就比较这两个点了。所以你可以看到,范数它其实是一个函数,它把不能比较的向量转换成可以比较的实数。