CCPC[长春] 2.Fraction 手动模拟

原 作者 楚东方 | 发表于 | 分类于 2015级

Fraction

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 0    Accepted Submission(s): 0

Problem Description
Mr. Frog recently studied how to add two fractions up, and he came up with an evil idea to trouble you by asking you to calculate the result of the formula below:


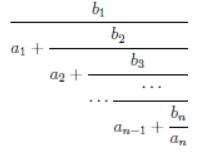
As a talent, can you figure out the answer correctly?
 

Input
The first line contains only one integer T, which indicates the number of test cases.

For each test case, the first line contains only one integer n ( n≤8).

The second line contains n integers:  a1,a2,⋯an(1≤ai≤10).
The third line contains n integers:  b1,b2,⋯,bn(1≤bi≤10).
 

Output
For each case, print a line “Case #x: p q”, where x is the case number (starting from 1) and p/q indicates the answer.

You should promise that p/q is irreducible.
 

Sample Input 

  

   1 2 1 1 2 3
  
 
 
 
 

   
 
 
 

 

   Sample Output
 
 
 
 
  

  

   Case #1: 1 2 
   

    

     Hint
    
 Here are the details for the first sample: 2/(1+3/1) = 1/2 
   

  
 
 
 
 

   
 
 
 

 
 
  Statistic | 
  Submit | 
  Clarifications | 
  Back
 
 
 


 
 



 


 

直接手动模拟，上代码
 



#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <climits>
#include <cstring>
#include <string>
#include <set>
#include <map>
#include <queue>
#include <stack>
#include <vector>
#include <list>
#define rep(i,m,n) for(i=m;i<=n;i++)
#define rsp(it,s) for(set<int>::iterator it=s.begin();it!=s.end();it++)
const int inf_int = 2e9;
const long long inf_ll = 2e18;
#define inf_add 0x3f3f3f3f
#define mod 1000000007
#define vi vector<int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define PI acos(-1.0)
#define pii pair<int,int>
#define Lson L, mid, rt<<1
#define Rson mid+1, R, rt<<1|1
const int maxn=5e2+10;
using namespace std;
typedef  long long ll;
typedef  unsigned long long  ull; 
inline int read(){int ra,fh;char rx;rx=getchar(),ra=0,fh=1;
while((rx<'0'||rx>'9')&&rx!='-')rx=getchar();if(rx=='-')
fh=-1,rx=getchar();while(rx>='0'&&rx<='9')ra*=10,ra+=rx-48,
rx=getchar();return ra*fh;}
//#pragma comment(linker, "/STACK:102400000,102400000")
ll gcd(ll p,ll q){return q==0?p:gcd(q,p%q);}
ll qpow(ll p,ll q){ll f=1;while(q){if(q&1)f=f*p;p=p*p;q>>=1;}return f;}
int dir[4][2]={{1,0},{-1,0},{0,1},{0,-1}};


ll a[100];
ll b[100];
int main()
{
    int T,n,k,i,j;
    scanf("%d",&T);
    for(k=1;k<=T;k++)
    {
        memset(a,0,sizeof(a));
        memset(b,0,sizeof(b));
        ll p,q,pt,qt;
        scanf("%d",&n);
        for(i=1;i<=n;i++)
            scanf("%lld",&a[i]);
        for(i=1;i<=n;i++)
            scanf("%lld",&b[i]);
        ll t;
        
        p=b[n];
        q=a[n];
        
        for(i=n-1;i>=1;i--)
        {
            p += q*a[i];
            
            pt=p;
            qt=q;
            
            q=pt;
            p=qt*b[i];
        }
        
        t = gcd(p,q);
        p /= t;
        q /= t;
        printf("Case #%d: %lld %lld\n",k,p,q); 
    }
     
    return 0;
}