分治——棋盘覆盖问题
在一个2k x 2k ( 即:2^k x 2^k )个方格组成的棋盘中,恰有一个方格(黑)与其他方格(白)不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。在棋盘覆盖问题中,要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。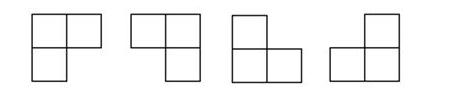
这里我们用分治法解决该问题。分治法是把一个规模很大的问题分解为多个规模较小、类似的子问题,然后递归地解决所有子问题,最后再由子问题的解决得到原问题的解决。
思路:
先把原方块分成四块,而黑色的那一块一定在其中一块中,为了递归求解,我们在其他三块上分别在原方块中心处填上一个方块,而这三个方块正好组成了一个L型骨牌。也就是填上了一个,用一个数进行标记,以后处理方式与此相同,我们进行递归求解。
下面上代码:
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<stdlib.h>
using namespace std;
int tile=1;//标志序号,根据其可以组成方块
int board[100][100];//用于记录
void chessBoard(int tr/*开始x坐标*/, int tc/*开始y坐标*/, int dr/*黑色x坐标*/, int dc/*黑车y坐标*/, int size)
{
if(size==1)//当其大小为1是返回
return;
int t=tile++;
int s=size/2;//分为4个
if(dr<tr+s && dc<tc+s)//判断黑色格是否在左上角的区域
chessBoard(tr, tc, dr, dc, s);//在则直接继续递归
else//否则,另右下角格变为黑,并给其赋t值
{
board[tr+s-1][tc+s-1]=t;
chessBoard(tr, tc, tr+s-1, tc+s-1, s);
}
if(dr<tr+s && dc>=tc+s)//右上角区域
chessBoard(tr, tc+s, dr, dc, s);
else
{
board[tr+s-1][tc+s]=t;//区域左下赋t值
chessBoard(tr, tc+s, tr+s-1, tc+s, s);
}
if(dr>=tr+s && dc<tc+s)//左下角区域
chessBoard(tr+s, tc, dr, dc, s);
else
{
board[tr+s][tc+s-1]=t;//区域右下赋t值
chessBoard(tr+s, tc, tr+s, tc+s-1, s);
}
if(dr>=tr+s && dc>=tc+s)//右下角区域
chessBoard(tr+s, tc+s, dr, dc, s);
else
{
board[tr+s][tc+s]=t;//区域左下赋t值
chessBoard(tr+s, tc+s, tr+s, tc+s, s);
}
//每执行一遍就相当与往上面填上了个图形。
}
int main()
{
int size;
printf("输入棋盘的size(大小必须是2的n次幂): ");
scanf("%d",&size);
int index_x,index_y;
printf("输入特殊方格位置的坐标: ");
scanf("%d %d",&index_x,&index_y);
chessBoard(0,0,index_x,index_y,size);
for(int i=0;i<size;i++)
{
for(int j=0;j<size;j++)
printf("%4d",board[i][j]);
printf("\n");
}
return 0;
}
