插值基函数:
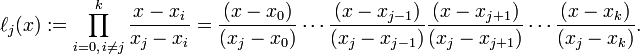
这玩意不知道是啥的话,没关系,简单看一下插值法从一次,二次,到n次推倒过程,到n阶就是上面那一坨..
线性插值也叫两点插值,已知函数y = f (x)在给定互异点x0, x1上的值为y0= f (x0),y1=f (x1)线性插值就是构造一个一次多项式
P1(x) = ax + b
使它满足条件
P1 (x0) = y0 P1 (x1) = y1
其几何解释就是一条直线,通过已知点A (x0, y0),B(x1, y1)。
线性插值计算方便、应用很广,但由于它是用直线去代替曲线,因而一般要求[x0, x1]比较小,且f(x)在[x0, x1]上变化比较平稳,否则线性插值的误差可能很大。为了克服这一缺点,有时用简单的曲线去近似地代替复杂的曲线,最简单的曲线是二次曲线,用二次曲线去逼近复杂曲线的情形。
拉格朗日插值时数学中最基本的插值算法,我们在差值时,如果插值点位于一直数据点之间,可以使用n次拉格朗日插值多项式来进行计算,如果插值点位于所给取件的某个端点时,可以少取几个数据点进行插值,如果差致电位于给定的区间以外,那么可以取最近的m个数据点进行插值.
拉格朗日插值法可以帮助我们解决以下的问题
已知x取值0,1,-1,2时, f{x}取值2,2,0,6
求x=3时f{x}的值。
示例1:
int xs[]={0,1,-1,2};
int ys[]={2,2,0,6};
//f(3)?
demo:
/*************************************************************************
> File Name: lagrange.cpp
> Author: dulun
> Mail: dulun@xiyoulinux.org
> Created Time: 2016年11月27日 星期日 16时57分43秒
************************************************************************/
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<algorithm>
#define LL long long
using namespace std;
const int N = 50086;
//x, y一一对应,共n对,按x升序排列, 插值点t
double Lagrange(double x[], double y[], int n, double t){
int i, j, k, m;
double s, result = 0.0;
if(n < 1) return result;
if(n == 1){
result = y[0];
return result;
}
if(n == 2){
result = ( y[0] * (t-x[1]) - y[1] * (t - x[0]) / x[0] - x[1] );
return result;
}
else{
i = 0;
while((x[i] < t) && (i < n)) i += 1;
k = i - 4;
if(k < 0) k = 0;
m = i + 3;
if(m > n-1) m = n-1;
for(i = k; i <= m; i++){
s = 1;
for(j = k; j <= m; j++){
if(j != i)
s = s*(t - x[j]) / (x[i] - x[j]);
}
result += s * y[i];
}
}
return result;
}
int main()
{
double t, z;
char again;
// static double x[] = {0.1, 0.15, 0.30, 0.4, 0.5, 0.6, 0.7, 0.85, 0.9, 1};
// static double y[] = {0.9, 0.86, 0.78, 0.67, 0.6, 0.55, 0.48, 0.42, 0.38, 0.36};
// 简单例子:y = f(x) = x^2
static double x[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
static double y[] = {1, 4, 9, 16, 25, 36, 49, 64, 81, 100};
//拽一下goto~
S1:
printf("Mission is a go!\nInput insert point: ");
cin>>t;
z = Lagrange(x, y, sizeof(x) / sizeof(x[0]), t);
cout << t << " : " << z << endl;
S2:
cout << "continue?(y/n)" << endl;
cin>>again;
if(again == 'y' || again == 'Y') goto S1;
else if(again == 'n' || again == 'N') goto S3;
else goto S2;
S3:
cout << "mission Success!" << endl;
return 0;
}