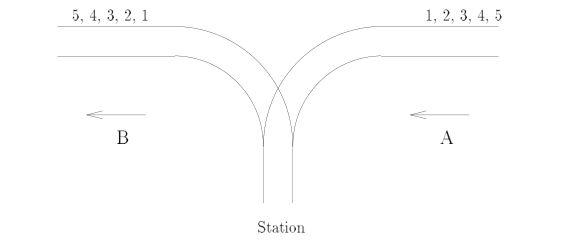
PopPush城市有一座著名的火车站。这个国家到处都是丘陵。而这个火车站是建于上一个世纪。不幸的是,那时的资金有限。所以只能建立起一条路面铁轨。而且,这导致这个火车站在同一个时刻只能一个轨道投入使用,因为它缺少空间,两列火车将无路可走。具体看下图。
当地的惯例是每一列火车从A方向驶向B方向时候,会用某种方式将车厢重组。假设火车将要到达A方向,拥有N个车厢(N<=1000),这些车厢按照递增顺序标记为1到N。负责从组车厢的领导,必须知道是否能从组车厢让它驶出B,而这个重组的序列就是a1\a2\a3…aN.帮组他并且写一个程序来判断是否可能按照所要求的车厢顺序。你可以假设,单个的车厢可以从列车上分离出来,在他们进入站台之前。并且他们可以自由移动,知道它们上了B轨道。你也可以假设在任意时候站台可以放下无数的车厢。但是只要一个车厢进入站台,它就不能返回A轨道,同时如果它离开了站台驶向B轨道,它就不能返回站台。
在中转站C中,车厢符合先进后出的原则,因此是一个栈。代码如下
#include<iostream>
#include<stdio.h>
#include<stack>
using namespace std;
const int MAXN = 1000 + 10;
int n, target[MAXN];
int main()
{
while(scanf("%d", &n) == 1) //输入 一共n辆火车
{
stack<int> s; //声明栈S
int A = 1, B = 1; // A:进站顺序 1,2,3,...,n B:出站顺序(数组target的下标)
for(int i = 1; i <= n; i++)
{
scanf("%d", &target[i]); //输入出站顺序
}
int ok = 1; //标志,是否可以按顺序出站
while(B <= n)
{
if(A == target[B]) //要进站的火车与要出站的火车为同一辆,则进站后直接出站
{
A++; B++;
}
else if(!s.empty() && s.top() == target[B]) //栈(站)非空,栈顶与要出站的火车相同,则出站
{
s.pop();
B++; //要出站的++
}
else if(A <= n) //要进站的与出站的不同,只进站,先等着,当栈顶与目标相同时再出(上一个if)
{
s.push(A++);
}
else
{
ok = 0; //正常结束循环为b=n, 若前几种情况都不符合,则不能按照要求顺序出站,break
break;
}
}
printf("%s\n", ok ? "Yes" : "No");
}
return 0;
}