GroupBlog

       KMP是Knuth-Morris-Pratt的简称，KMP算法是模式匹配当中的经典算法，也就是某大神说的“以某些人的名字命名”的算法，它是由D.E.Knuth,J.H.Morris和V.R.Pratt共同提出的一个改进算法。和BF（Brute Force）算法相比，KMP算法的优点在于当主串中的i指针失配时，不需要回溯到上一次开始匹配的下一个位置，而是利用已经得到的next数组将模式串中的j指针移动到尽可能向后的位置后，然后继续比较。

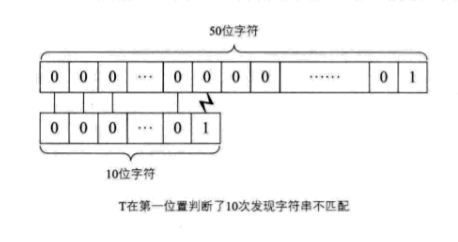
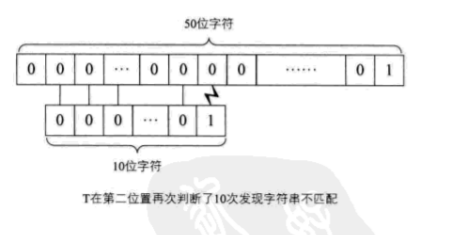
       举个例子，当主串S为“0000000000000000000000000000000000000001”，而要匹配的子串T为“0000000001”，如果用简单模式匹配算法，第一次匹配，直到i=j=10，发生失配，i要变为2,j要变为1,继续匹配，依次类推。每一次都是直到匹配到T串的最后一位，才会发现它们原来是不匹配的。



这样的话，显然要低效很多。

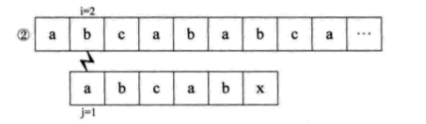
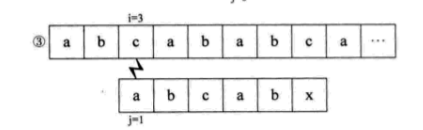
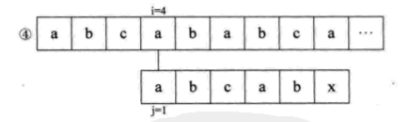
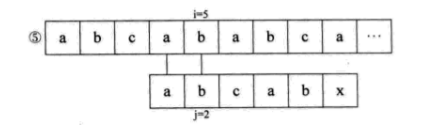
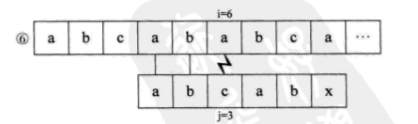
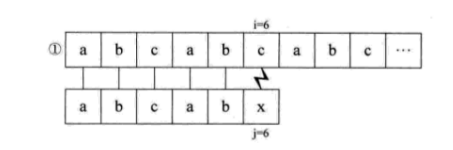
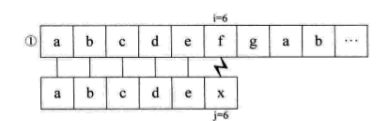
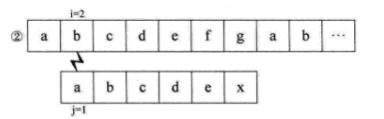
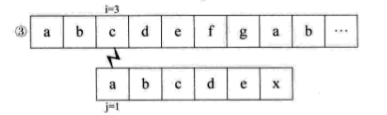
下面介绍KMP算法，假设主串S=“abcabcabc”,子串T=“abcabx”，从i=j=1开始匹配，直到匹配到i=j=6,出现失配。如果用简单模式匹配算法，流程如下。













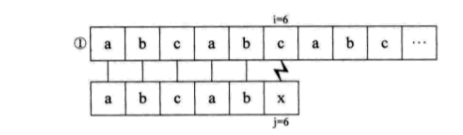
可是我们发现，S串中的第一个字母a与其后的b、c都是不相等的，也就是说，第 ②③步其实是多余的。又因为S串的前两位是ab，与j=4和j=5的ab一样，所以其实第六第七步我们也可以省略不用比较，直接从i=6、j=3开始比较。也就是说，我们可以直接从第一步跳到第六步。







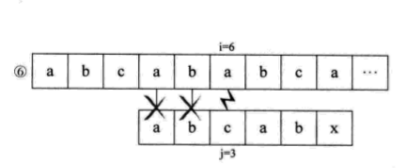
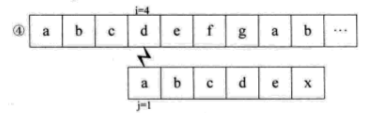
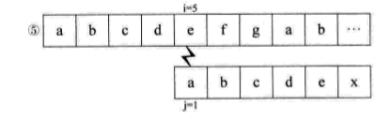
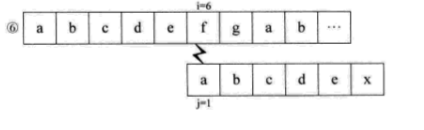
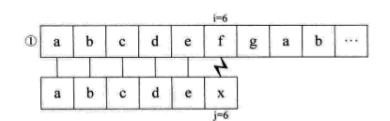
如果没有明白，就再看一个例子，假设主串S=“abcdefgab”，子串T=“abcdex”。用BF匹配，流程如下:













当比较到i=j=6，失配时，我们会发现，子串S的首字符a与j=2,3,4,5时的bcde都不相等，也就是说，当i=j=6之前都匹配了的时候，说明S串中的a与T串中i=2,3,4,5时的bcde不匹配，所以，上面流程中的② ③ ④ ⑤步是不需要的。当i=j=6失配时，我们可以直接跳到i=6,j=1开始匹配。





通过上面的例子，我们可以发现，在字符串比较时，主串T的i值是一直增加的，没有回溯，只有子串S的j值一直在不停的改变，并且每次回溯的值都是不一样的，这个j每次要回溯的值，就是我们需要提前求好的next [ ]数组，这也是KMP算法的关键。

下面我先给出next[ ]数组的定义。

若令next[ j ]=k，那么next[ j ]表示当第j个字符与主串中相应的字符失配时，T串应从j=k的地方开始下一次匹配。

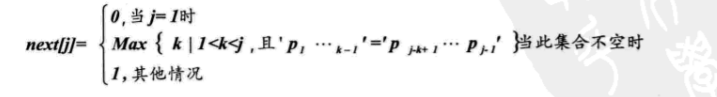
光看公式，可能不太好理解，用语言来表达，就是当指针i和j在j=j这个位置失配时，在子串T的字符j之前的j-1个字符串中，前k-1个字符串，与后k-1个字符串完全相等（可重叠），那么就让j的值等于k，继续进行下一次匹配，即next[ j ]=k。

举几个例子：

eg1:abcabx

next[1]=0;   因为j=1时，next[1]=0.

next[2]=1;   因为j=2时，前j-1个字符串即a中，没有相等的字符串，所以属于其他情况，即next[2]=1;

next[3]=1;   因为j=3时，前j-1个字符串即ab中，没有相等的字符串，所以属于其他情况，即next[3]=1;

next[4]=1;   因为j=4时，前j-1个字符串即abc中，没有相等的字符串，所以属于其他情况，即next[3]=1;

next[5]=2;   因为j=5时，前j-1个字符串即abca中，第一个a与最后一个a相等，所以k=2，即next[5]=2;

next[6]=3;   因为j=6时，前j-1个字符串即abcab中，前两个字符ab与后两个字符ab相等，所以k=3;即next[5]=3。

eg2:ababaaaba

next[1]=0;   因为j=1时，next[1]=0.

next[2]=1;   因为j=2时，前j-1个字符串即a中，没有相等的字符串，所以属于其他情况，即next[2]=1;

next[3]=1;   因为j=3时，前j-1个字符串即ab中，没有相等的字符串，所以属于其他情况，即next[3]=1;

next[4]=2;   因为j=4时，前j-1个字符串即aba中，第一个a与最后一个a相等，所以k=2，即next[4]=2;

next[5]=3;   因为j=5时，前j-1个字符串即abab中，前两个字符ab与后两个字符ab相等，所以k=3;即next[5]=3;

next[6]=4;   因为j=6时，前j-1个字符串即ababa中，前三个字符aba与后三个字符aba相等，所以k=4;即next[6]=4：

next[7]=2;   因为j=7时，前j-1个字符串即ababaa中，第一个a与最后一个a相等，所以k=2，即next[7]=2;

next[8]=2;   因为j=8时，前j-1个字符串即ababaaa中，第一个a与最后一个a相等，所以k=2，即next[8]=2;

next[9]=3;   因为j=9时，前j-1个字符串即ababaaab中，前两个字符ab与后两个字符ab相等，所以k=3;即next[9]=3;

eg3：aaaaab

next[1]=0;   因为j=1时，next[1]=0.

next[2]=1;   因为j=2时，前j-1个字符串即a中，没有相等的字符串，所以属于其他情况，即next[2]=1;

next[3]=2;   因为j=3时，前j-1个字符串即aa中，第一个a与最后一个a相等，所以k=2，即next[3]=2;

next[4]=3;   因为j=4时，前j-1个字符串即aaa中，前两个字符aa与后两个字符aa相等，所以k=3;即next[4]=3;

next[5]=4;   因为j=5时，前j-1个字符串即aaaa中，前三个字符aaa与后三个字符aaa相等，所以k=4;即next[5]=4：

next[6]=5;   因为j=6时，前j-1个字符串即aaaaa中，前四个字符aaaa与后四个字符aaaa相等，所以k=5;即next[6]=5：

下面是next[ ]数组的代码实现：
#include <stdio.h>

void get_next(char *T,int *next,int n)
{
	int j=1,k=0;
	next[1]=0;
	while(j <= n)
	{
		if(k==0 || T[k]==T[j])
		{
			++k;
			++j;
			next[j]=k;
		}
		else
		{
			k=next[k];
		}
	}	
}

int main()
{
	int i,n;
	printf("please input the length of T:");
	scanf("%d",&n);
	getchar();
	int next[n];
	char T[n];
	printf("please input string T:\n");
	for(i=1; i<=n; i++)
	{
		scanf("%c",&T[i]);
	}
	get_next(T,next,n);
	for(i=1; i<=n; i++)	      
	{
		printf("%d",next[i]);
	}
	printf("\n");
	return 0;
}
运行结果如下：

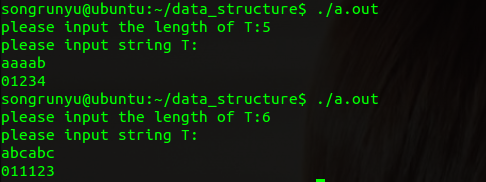
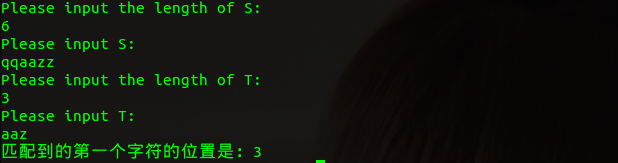
next数组求完，KMP算法的核心内容就已经基本结束了，接下来就只需要利用next数组来求出匹配的位置，完整代码实现如下：
#include <stdio.h>

void get_next(char *T,int *next,int m)
{
	int j=1,k=0;
	next[1]=0;
	while(j <= m )
	{
		if(k==0 || T[k]==T[j])
		{
			++j;
			++k;
			next[j]=k;
		}
		else
		{
			k=next[k];
		}
	}
}

int Index_KMP(char *S, int pos, char *T, int n, int m)
{
	int i=pos,j=1;        //主串从第pos开始，模式串从头开始
	int next[m];
	get_next(T, next, m);
	while(i <= n && j <= m)
	{
		if(j==0 || S[i]==T[j])
		{
			++i;
			++j;
		}
		else
		{
			j=next[j];
		}
	}
	if(j > m)
	      return i-m;
	else 
	      return 0;
}

int main(int argc, char *argv[])
{
	int i,n,m,t;

	printf("Please input the length of S:\n");
	scanf("%d",&n);
	getchar();
	char S[n];
	printf("Please input S:\n");
	for(i=1; i<=n; i++)
	      scanf("%c",&S[i]);
	getchar();

	printf("Please input the length of T:\n");
	scanf("%d",&m);
	getchar();
	char T[m];
	printf("Please input T:\n");
	for(i=1; i<=m; i++)
	      scanf("%c",&T[i]);

	t = Index_KMP(S,1,T,n,m);
	if(t)
	{
		printf("匹配到的第一个字符的位置是：%d\n",t);
	}
	else
	{
		printf("匹配失败！\n");
	}
	return 0;

}
运行结果：

关于字符串匹配的算法，除了本篇博客中提到的BF，KMP算法之外，还有BM,Sunday算法，这两种算法比KMP还要快，有感兴趣的可以去查阅相关资料。