构造一棵二叉排序树的目的,其实并不是为了排序,而是为了提高查找和插入删除的效率。
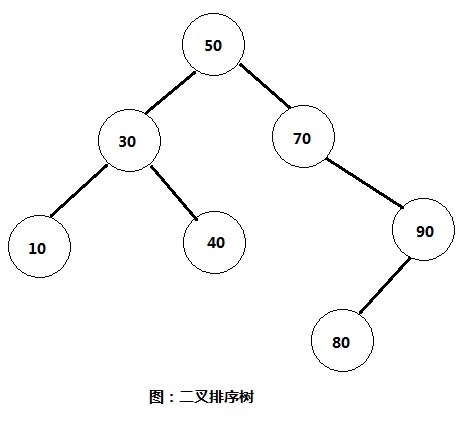
那么什么是二叉排序树呢?二叉排序树具有以下几个特点:
1,若根节点有左子树,则左子树的所有节点都比根节点小;
2,若根节点有右子树,则右子树的所有节点都比根节点大;
3,根节点的左,右子树也分别为二叉排序树.
插入
思路:首先查找待插入的记录是否在树中,如果存在则不允许插入重复关键字;如果直到找到叶子结点扔没有发现重复关键字,则把待插结点作为新的叶子结点插入.
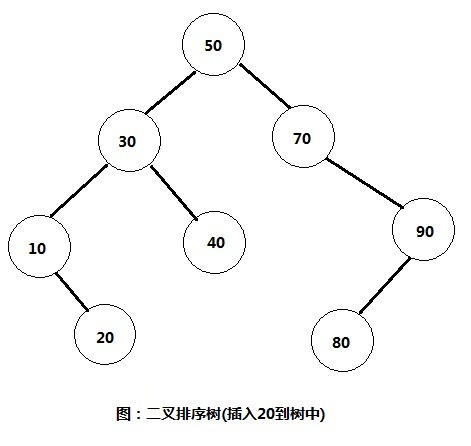
比如我们要插入数字20到这棵二叉排序树中。那么步骤如下:
1) 首先将20与根节点进行比较,发现比根节点小,所以继续与根节点的左子树30比较。
2) 发现20比30也要小,所以继续与30的左子树10进行比较。
3) 发现20比10要大,所以就将20插入到10的右子树中。
查找
思路:
1)若给定的值等于根结点的关键字,则查找成功.
2)如给定的值小于根结点的关键字,则继续在左子树上查找
3)如给定的值大于根结点的关键字,则继续在右子树上查找
比如我们要查找节点10,那么思路如下:
1) 首先将10与根节点50进行比较大小,发现比根结点要小,所以继续与根节点的左子树30进行比较。
2) 发现10比左子树30要小,所以继续与30的左子树10进行比较。
3) 发现两值相等,即查找成功,返回10的位置。
删除
删除结点的情况相对复杂,主要分以下三种情形:
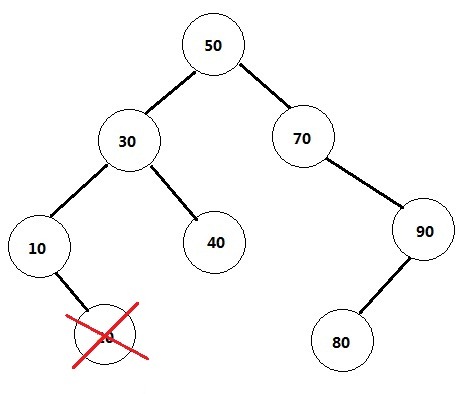
1) 删除的是叶结点(即没有孩子节点的)。比如20,删除它不会破坏原来树的结构,最简单。如图所示。
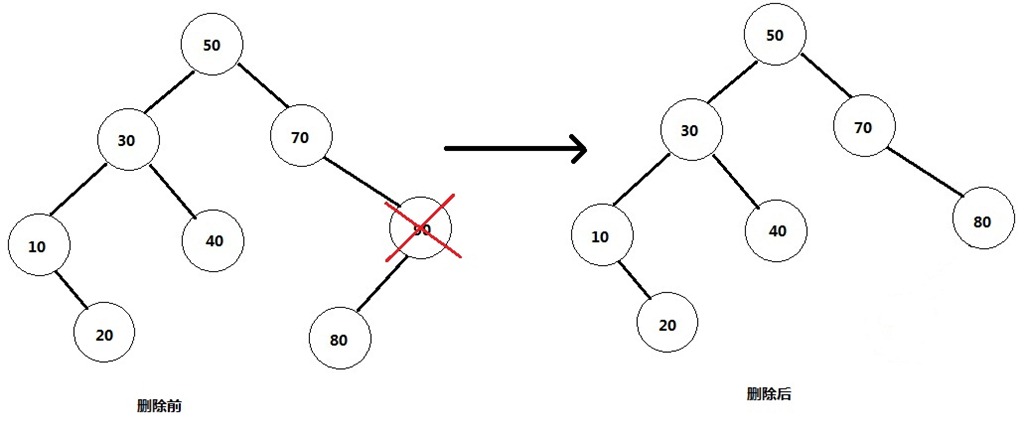
2) 删除的是单孩子结点。比如90,删除它后需要将它的孩子结点与自己的父结点相连。情形比第一种复杂一些。
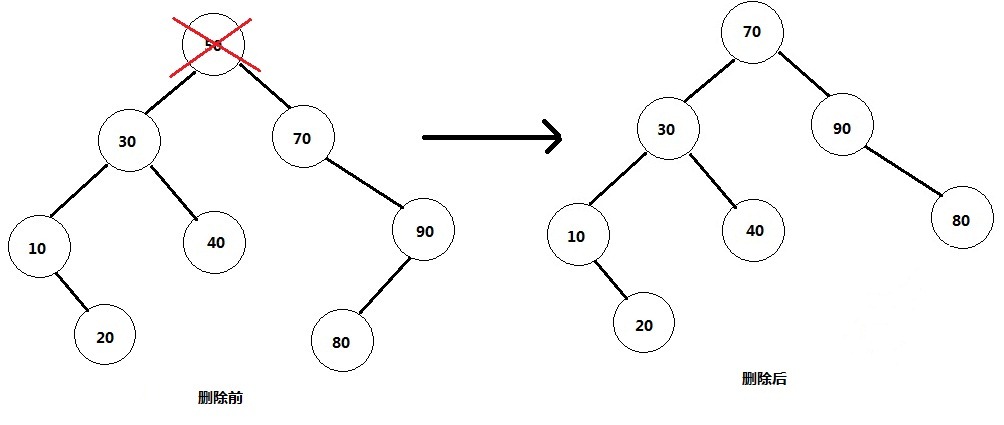
3) 删除的是有左右孩子的结点。比如根结点50,这里有一个问题就是删除它后将谁做为根结点的问题?利用二叉树的中序遍历,就是其前驱结点或后继结点,这样保证了其他元素的移动量是最小的,即保证删除的高效性.
性能
二叉排序树的查找最差的情况与顺序查找相同,ASL=(n+1)/2;
最好的情况与折半查找相同ASL = logN.