题目:在 O(n log n) 时间复杂度和常数级空间复杂度下,对链表进行排序。
示例 1:
输入: 4->2->1->3
输出: 1->2->3->4
示例 2:
输入: -1->5->3->4->0
输出: -1->0->3->4->5
思路
题中给的时间复杂度让你进行排序,基本都可以想到归并排序,但本题目复杂的地方就在于是链表数据,所以如何进行链表的分开和合并就是难点
分析
1、使用自下而上的归并排序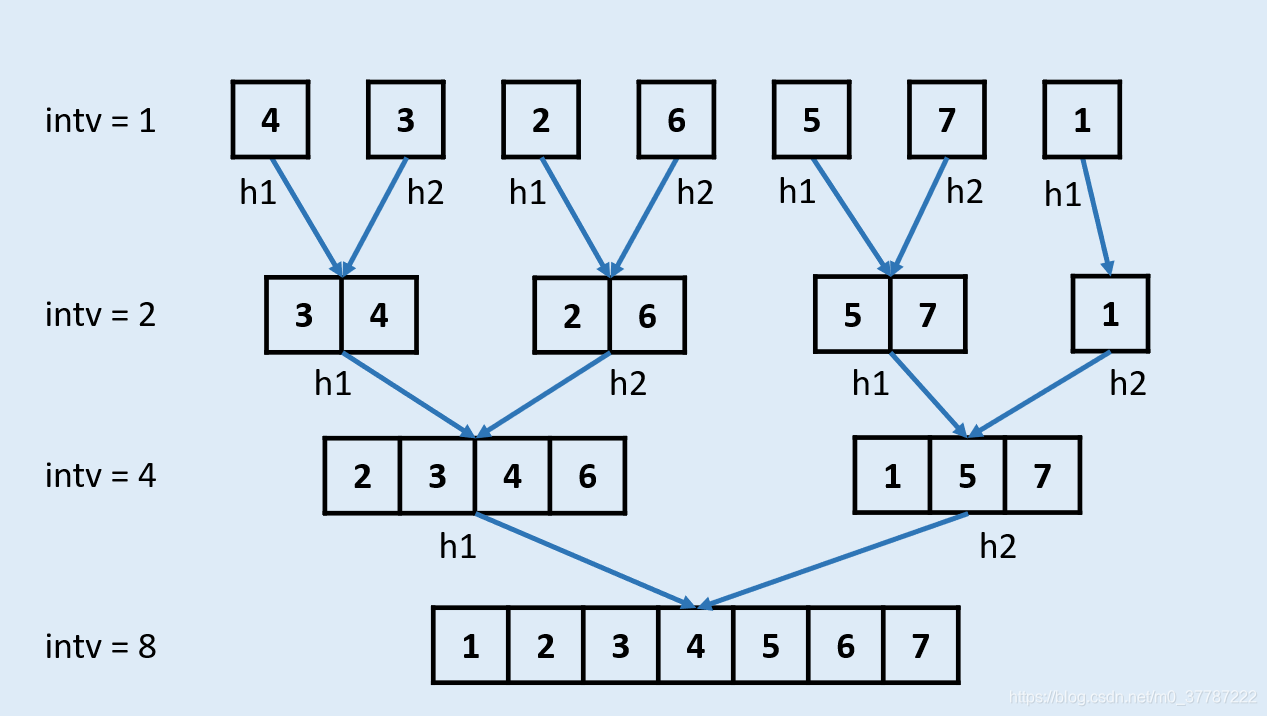
使用二路归并就是先进行两个合并,之后四个合并,下来八个合并,所以合并的步数长就是step*=2
2、进行分割的cut函数
cut(pos, step)
将链表 pos切掉前 step个节点,并返回后半部分的链表头,目的就是进行断链
3、merge函数
归并的merge函数基本都是一样的,但是本题使用了dummyHead这个网上称作的一个数据结构,其实它存在的目的就是因为本题head存有数据,不能直接当头结点使用,有了dummyHead这个空指针之后,既可以把dummyHead当做一个新的链表使用,也可以为合并后的链表提供一个头结点
duummyHead参考资料
https://www.jianshu.com/p/e8103ebff64c
https://www.cnblogs.com/make-big-money/p/10321425.html
题解
(建议复制到所用编辑器,系统给的这个颜色注释看不清)
class Solution
{
public:
ListNode *sortList(ListNode *head)
{
ListNode dummyHead(0);//相当于设置一个头结点
dummyHead.next = head;//因为题目给的head本身就存有数据
auto p = head;
int length = 0;
while (p)//得出链表长度
{
++length;
p = p->next;
}
for (int step = 1; step < length; step*=2)//也可以用左赋值语句 step <<= 1
{
auto cur = dummyHead.next;
auto p = &dummyHead;
while (cur)
{
auto left = cur;
auto right = cut(left, step);
//left后step步后是一个新断链开始
cur = cut(right, step);
//检测right之后step步之后是否存在断链
p->next = merge(left, right);//把合并好的链表放在p之后
while (p->next)
//移动到已经排序好链表的最后一个,方便下次的插入
p = p->next;
}
}
return dummyHead.next;
}
ListNode *cut(ListNode *head, int n)
{
auto p = head;
while (--n && p)
p = p->next;
if (!p)//n步之后为空就证明不能再分割
return nullptr;
auto cut_next = p->next;//下一个分割点的开头
p->next = nullptr;
//将分割点下一个节点变为空,就可以保证是分割开的一段段链表
return cut_next;
}
ListNode *merge(ListNode *left, ListNode *right)
{
ListNode dummyHead(0);
auto p = &dummyHead;
//dummyHead本来就是没有用过,相当于复用这个头结点
while (left && right)
{
if (left->val < right->val)//left的值小就进行插入
{
p->next = left;
p = left;
left = left->next;
}
else//right的值小就进行插入
{
p->next = right;
p = right;
right = right->next;
}
}
p->next = left ? left :right;
//直接把剩余的链表插入
return dummyHead.next;
}
};