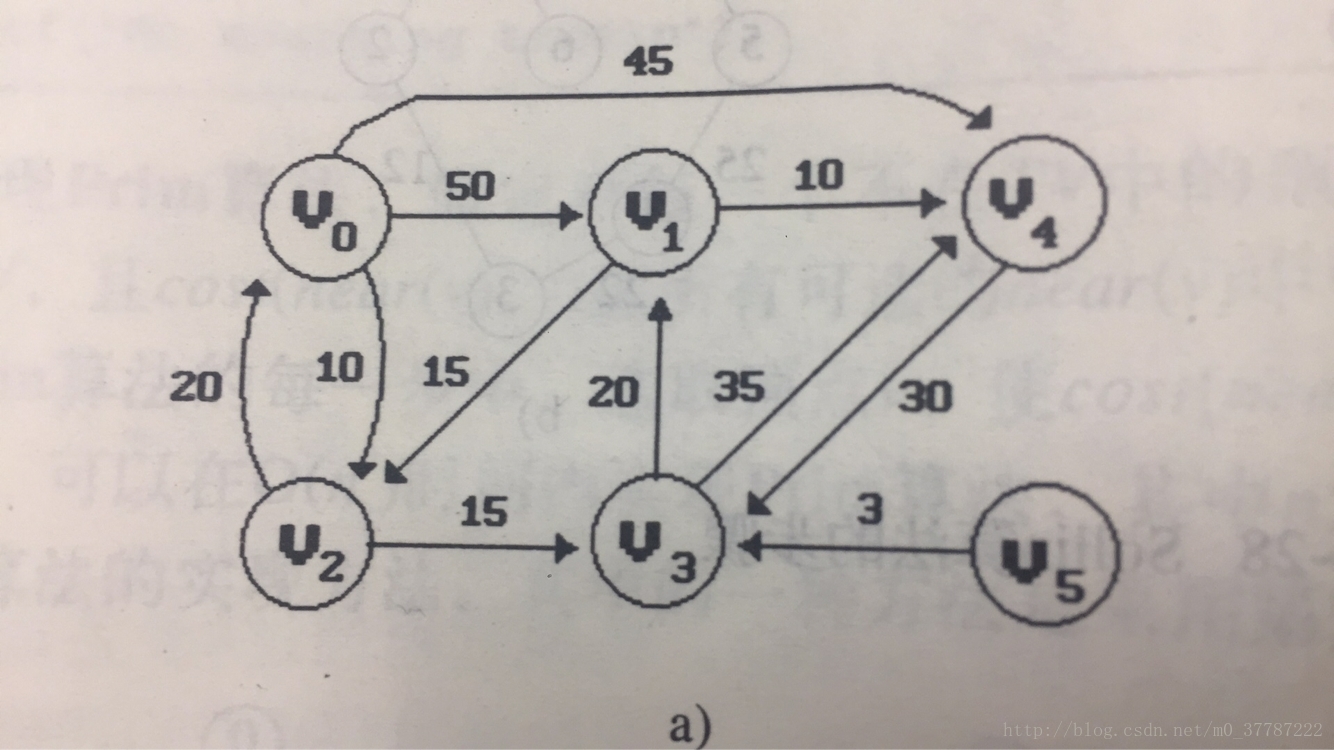
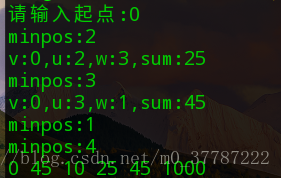
思路:
①随意选择一个点v,然后用distance数组记录起始点v到所有点的距离
②然后在distance数组中找到起始点v到哪一个点的距离最短,以这个点u为中介,found[u]=1,证明集合中已经有这个点,证明该点走过
③使用choose函数通过循环,可以知道哪一个点到起始点最短,返回该点的索引u
④然后再以u这个点开始,去没有走过的点w(found数组中没有标记为1的点)一一试探,只要distance[u]到某一点w的距离(即distance[u]+cost[u][w] )小于w到起始点的距离(distance[w]),则修改distance[w],即distance[w]是到起始点v的最小距离
#include<stdio.h>
#define MAX 6
int cost[][MAX] =
{
{ 0, 50, 10,1000, 45,1000},
{1000, 0, 15,1000, 10,1000},
{ 20,1000, 0, 15,1000,1000},
{1000, 20,1000, 0, 35,1000},
{1000,1000, 30,1000, 0,1000},
{1000,1000,1000, 3,1000, 0}
};//表示图的对应值1000证明不能连通
int n = MAX;
int found[50] = {0};//记录已经做过的点,0表示没走过
int distance[50] = {0};//表示起点到个点距离
void shortestpath(int v,int cost[][MAX],int distance[],int n,int found[]);
int choose(int distance[],int n,int found[]);//选择最短距离
int main()
{
int v;
printf("请输入起点:");
scanf("%d",&v);
shortestpath(v,cost,distance,n,found);
for(int i=0;i<n;i++)//最终结果
{
printf("%d ",distance[i]);
}
putchar('\n');
return 0;
}
void shortestpath(int v,int cost[][MAX],int distance[],int n,int found[])
{
int u,w;
for(int i = 0;i < n;i++)//初始化起点到所有点的距离
{
found[i] = 0;
distance[i] = cost[v][i];
}
found[v] = 1;
distance[v] = 0;
for(int i = 0;i < n-2;i++)//因为每次distance是加两个,所以只能少两个-2
{
u = choose(distance,n,found);//找最小距离点,之后u变成一个中间点
if(u == -1)
continue;
found[u] = 1;//加入集合中了
for(w = 0;w < n;w++)
{
if(!found[w])//如果改点没走过,distance还就不是最短
{
if(distance[u]+cost[u][w]< distance[w])//如果distance[u]加cost[u][w]小于distance[w],就改distance[w]值
{
distance[w] = distance[u]+cost[u][w];
}
}
}
}
}
int choose(int distance[],int n,int found[])
{
int min = 9999;
int minpos = -1;
for(int i=0;i < n;i++)
{
if(distance[i] < min && !found[i])
{
min = distance[i];
minpos = i;
}
}
printf("minpos:%d\n",minpos);
return minpos;
}