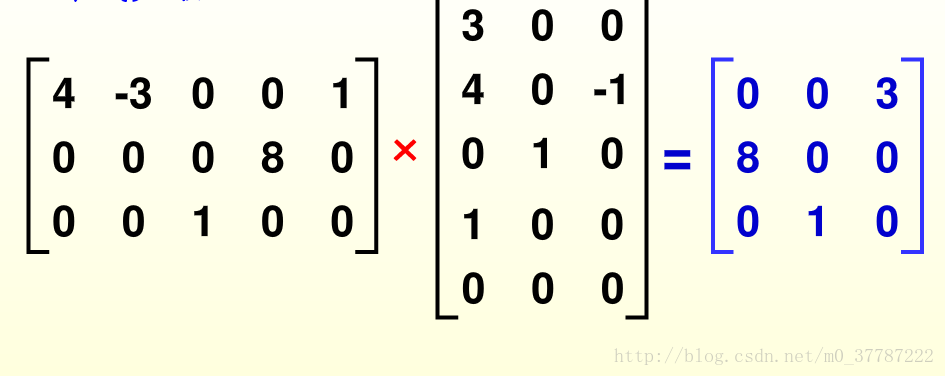
被这个稀疏矩阵折磨了很久,看了将近一个半礼拜,看的我很想撕书。
这个是程序思想是和数据结构(c语言版)机械工业出版社的学习的,书 代码讲解不是很详细,搜了网上很多代码,都是抄了一下,草草注释,在我自己写的时候发现书上的代码是有问题的。
书上p48,new_b使用int类型,但是转置是term类型,而且转置都是用了一位数组。
还有就是书上的边界条件处理的是有问题的,如果原封不动的写,最后结果会是两行叠加的答案,我写了两种方法
书上显然是错的,查了很多中文版本,代码都是错的,没有查到英文版,不知道是什么状况,有哪位看到英文版的代码,请给我发一下原版,不胜感激!!!
都说国外书很好,但是我觉得还是自己多动手,不能光看,尽信书不如无书,这个题也警示我要多动手!!!
大家只要耐心的看程序下面的图就可以大概了解过程,过程图是我自己画的,画的不是太好,如果大家觉得这篇博客可以帮到你,大家可以随意转载,能帮到大家非常开心,写的不对的地方希望大家提出来,希望和大家一起进步!!!
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define MAX_TERMS 101
#define MAX_COL 50
typedef struct{
int col;
int row;
int value;
}term;
term a[MAX_TERMS];
term b[MAX_TERMS];
term d[MAX_TERMS];
void fast_transpose(term a[],term b[]);
void mmult(term a[],term b[],term d[]);
int compare(int a,int b);
void storesum(term d[],int *totald,int row,int column,int *sum);
int main()
{
int value;
int count = 1;
printf("请输入将要输入a矩阵的行和列数\n");
scanf("%d%d",&a[0].row,&a[0].col);
printf("请输入数据\n");
for(int i = 1;i <= a[0].row;i++)
for(int j = 1;j <= a[0].col;j++)
{
scanf(" %d",&value);
if(value != 0)
{
a[count].row = i;
a[count].col = j;
a[count].value = value;
count++;
}
}
a[0].value = count-1;
count = 1;
printf("请输入将要输入b矩阵的行和列数\n");
scanf("%d%d",&b[0].row,&b[0].col);
printf("请输入数据\n");
for(int i = 1;i <= b[0].row;i++)
for(int j = 1;j <= b[0].col;j++)
{
scanf(" %d",&value);
if(value != 0)
{
b[count].row = i;
b[count].col = j;
b[count].value = value;
count++;
}
}
b[0].value = count-1;
mmult(a,b,d);
for(int i=1; i <= d[0].value;i++)//最后输出结果
printf("%d %d value is %d\n",d[i].row,d[i].col,d[i].value);
}
void fast_transpose(term a[],term b[])//转置
{
int row_term[MAX_COL],starting_pos[MAX_COL];
int i,j,num_cols=a[0].col,num_terms = a[0].value;
b[0].row = num_cols;b[0].col = a[0].row;
b[0].value = num_terms;
if(num_terms > 0)//非零矩阵
{
memset(row_term,0,sizeof(row_term));
for(int i =1;i <= num_terms;i++)//个数取决于a中非零元素个数
row_term[a[i].col]++;
starting_pos[0]=1;
for(int i = 1;i <= num_cols;i++)
starting_pos[i] = starting_pos[i-1] + row_term[i-1];
for(int i = 1;i <= num_terms;i++)
{
j=starting_pos[a[i].col]++;
b[j].row = a[i].col;b[j].col = a[i].row;
b[j].value = a[i].value;
}
}
}
void mmult(term a[],term b[],term d[])
{
int i,j,column,totalb = b[0].value,totald = 0;
int rows_a = a[0].row,cols_a = a[0].col;
int totala = a[0].value,cols_b = b[0].col;
int row_begin = 1,row = a[1].row,sum = 0;
term new_b[MAX_TERMS];
if(cols_a !=b[0].row)
{
fprintf(stderr,"Incompatible matrices\n");
exit(1);
}
fast_transpose(b,new_b);
//因为b三元组转置之后,a和b就可以直接行和行相乘,方便操作
a[totala+1].row = rows_a;
new_b[totalb+1].row = cols_b + 1;
//哨兵存在的意义就是有可能一个三元组计算完,另一个三元组不能计算
// ↑方法一: 改变哨兵条件,当进入哨兵位置时,哨兵给予一个不存在的行(大于所有行)
// 此时当j=totalb+1时会进入else if(new_b[j].row!=column)这一句,自动存储本列的乘积
new_b[totalb+1].col = 0;
//转置的三元组有一个超过本来长度的元素好处是
//进入下面的compare函数,j++,代表又有一列结束,需要sum++
//不然就会出现上一行结果和下一行结果相加的情况
for(i = 1;i <= totala;)
{
column = new_b[1].row;
for(j = 1;j <= totalb + 1;)
{
if(a[i].row!=row)//a三元组和开始的行号不等,证明左边矩阵需要换行,进行sum
{
storesum(d,&totald,row,column,&sum);
i = row_begin;
for(;new_b[j].row == column;j++)
;
column = new_b[j].row;//a要更新一行和b的起始相乘;
}
else if(new_b[j].row!=column)
{
storesum(d,&totald,row,column,&sum);
i = row_begin;
column = new_b[j].row;
}
else switch(compare(a[i].col,new_b[j].col))
{
case -1 :
i++;
break;
case 0:
sum +=(a[i].value*new_b[j].value);
i++; j++;
break;
case 1:
j++;
break;
}
// 方法二:当执行到哨兵位置时,说明即将换列,此时将本列的乘积存储起来
// if (j == totalb + 1)
// {
// storesum(d,&totald,row,column,&sum);
// }
}
//a需要换行,所有一旦不满足现在的行号,证明换行成功
for(;a[i].row == row;i++)
;
row_begin = i;//a的新的开始
row = a[i].row;//新行号
}
d[0].row = rows_a;//将最后的非零元素统计
d[0].col = cols_b;
d[0].value = totald;
}
int compare(int a,int b)
{
if(a > b)
return 1;
if(a == b)
return 0;
if (a < b)
return -1;
}
void storesum(term d[],int *totald,int row,int column,int *sum)
{
if(*sum)//只有乘积不为零才记录
{
if(*totald < MAX_TERMS)//防止总共的d元素超过定义的最大数
{
d[++*totald].row = row;
d[*totald].col = column;
d[*totald].value = *sum;
*sum = 0;
}
else
{
fprintf(stderr,"Numbers of terms in product exceeds %d\n",MAX_TERMS);
exit(1);
}
}
}