DFS和BFS学习总结

DFS深度优先遍历

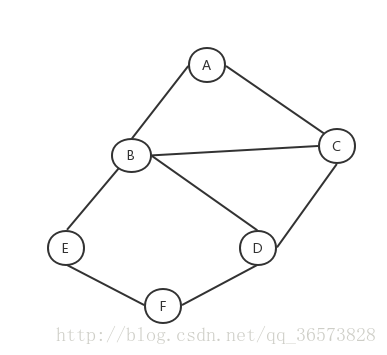
深度遍历就是在图中从一个顶点开始，按照一个规则不重复地走下去。就是不撞南墙不回头一样。假如从A顶点开始，按照一个规则去走（假如我们按照一直字典顺序走）那么就从A走到B再从B走到了C，走到C后再按照字典顺序的时候，发现A已经走过，那么此时就退回到C点，选择另一个D走下去。就和树的前序遍历是一样的。

实现方式

1、递归实现（通过邻接矩阵来实现）

void DFS(MGrap G. int i)
{
    int j = 0;
    visited[i] = 1;
    count++;
    for(j=0; j<G.numVertexes; j++)
    {
        if(G.arc[i][j]==1 && !visited[j])//i和j有关系相邻，并且j顶点没有被访问过
        {
            DFS(G, j);
        }
    }
}

void dfs(MGrap G,int v)  
{  
    init(&s);//使用自定义栈之前对栈进行初始化  
    push(&s,v);  //入栈第一个元素
    while(!isEmpty(&s))  
    {  
        pop(&s,&v);  //取出栈顶元素
        if(!visit[v])  //若没有访问过
        {  
            cout<<v<<' '; //输出该顶点
            visit[v]=true;  //标记已经访问过
            for(int k=0;k<M;k++)  //查找与该顶点相关联的顶点
            {  
                if(!visit[k]&&g[v][k]==1)  //若果未被访问过，且有相连的边
                {  
                    /*入栈操作*/
                    push(&s,k);  
                }  
            }  
        }  
    }  

}  

BFS广度 优先搜索遍历

类似于树的层次搜索，主要是从图中的某个顶点出发，在访问此顶点后，依次访问未被访问的邻接顶点。

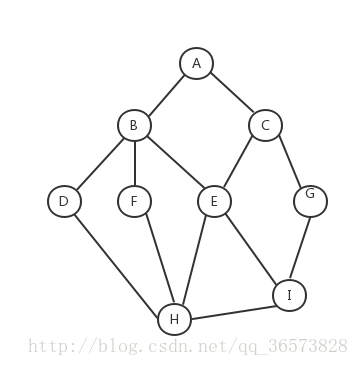
以A为开始节点，依次遍历B，C，再从B相邻的结点DFE开始遍历，最后遍历的结果就是：ABCDFEGHI（遵循先进先出规则）

实现（采用邻接矩阵）

1、采用队列的方式

void BFS(MGrap G)
{
    int i,j;
    Queue Q;
    for(i=0; i<G.numVertexes; i++)/*初始化访问数组*/
    {
        visited[i] = -1;
    }
    InitQueue(&Q);
    for(i=0; i<G.numVertexes; i++)
    {
        if(!visited[i])
        {
            visited[i] = 1;
            printf("%c",G.vexs[i]);
            EnQueue(&Q,i);/*入队操作*/
            while(!QueueEmpty(Q))
            {
                DeQueue(&Q, &i);
                for(j=0; j<G.numVertexes; j++)
                {
                    /* 判断当前的节点与其他节点的关系 */
                    if(G.arc[i][j]==1 && !visited[j])
                    {
                        visited[j] = 1;
                        EnQueue(&Q,j);
                    }
                }
            }
        }
    }
}

---

总结：

两者的不同点是，BFS遍历的时候，按照深度去遍历，需要回退，所以需要用栈来记录原来顶点的位置；DFS是从相邻的结点开始依次遍历，所以先遍历到谁就先输出谁，所以采用队列的方式去实现。