GroupBlog

题目描述

请你为最不经常使用（LFU）缓存算法设计并实现数据结构。它应该支持以下操作：get 和 put。

get(key) - 如果键存在于缓存中，则获取键的值（总是正数），否则返回 -1。
put(key, value) - 如果键不存在，请设置或插入值。当缓存达到其容量时，则应该在插入新项之前，使最不经常使用的项无效。在此问题中，当存在平局（即两个或更多个键具有相同使用频率）时，应该去除最近最少使用的键。
「项的使用次数」就是自插入该项以来对其调用 get 和 put 函数的次数之和。使用次数会在对应项被移除后置为 0 。

进阶：
你是否可以在 O(1) 时间复杂度内执行两项操作？

示例：

LFUCache cache = new LFUCache( 2 /* capacity (缓存容量) */ );

cache.put(1, 1);
cache.put(2, 2);
cache.get(1);       // 返回 1
cache.put(3, 3);    // 去除 key 2
cache.get(2);       // 返回 -1 (未找到key 2)
cache.get(3);       // 返回 3
cache.put(4, 4);    // 去除 key 1
cache.get(1);       // 返回 -1 (未找到 key 1)
cache.get(3);       // 返回 3
cache.get(4);       // 返回 4

解析

当缓存达到其容量时，则应该在插入新项之前，使最不经常使用的项无效。在此问题中，当存在平局（即两个或更多个键具有相同使用频率）时，应该去除最近最少使用的键。

首先看题目描述中的这句话，就可以知道我们需要设计数据结构时要有节点出现的频率，还有最近一次使用该节点的时间。这样才能确保当容器满的时候，我们能够正确的删除节点。

方法一：哈希表+平衡二叉树

我们自定义节点

    struct Value
    {   
        Value(int count_, int time_, int key_, int value_)
         : count(count_), 
           key(key_), 
           value(value_), 
           time(time_) {}
        //重载小于运算符，为了set排序时使用
        bool operator < (const Value& a) const 
        {
            return count == a.count ? time < a.time : count < a.count;
        }
        int key; 
        int value;
        int count;  //频率
        int time;   //时间
    };

在c++中，我们可以使用std::set来对节点进行排序。std::set底层是红黑树实现的(平衡二叉树的一种)。
哈希表我们就用unordered_map(其底层就是可扩展的拉链法实现的)。
在这里插入图片描述

对于get操作，我们需要检查哈希表中是否有该元素，如果没有就返回-1。有的话就需要更新Value中的频率和time，然后重新加入到set中。
对于put操作，我们也需要检查哈希表中是否有该元素。
没有的话，我们首先需要判断哈希表的容量是否等于LFU归定的容量，等于的话我们就需要将不活跃的从表中删除再进行插入，否则直接插入即可。
有该元素的话，其实操作和get很类似，只不过需要更新key对应的value的值。
代码实现。

    struct Value
    {   
        Value(int count_, int time_, int key_, int value_)
         : count(count_), 
           key(key_), 
           value(value_), 
           time(time_) {}
        bool operator < (const Value& a) const 
        {
            return count == a.count ? time < a.time : count < a.count;
        }
        int key;
        int value;
        int count;
        int time;
    };
class LFUCache 
{
public:
    LFUCache(int capacity_) 
    : capacity(capacity_),
    time(0) {}
    
    int get(int key) 
    {
        if(capacity == 0)
            return -1;
        auto it = table.find(key);
        if(it == table.end())
            return -1;
        Value cache = it->second;
        judge.erase(cache);
        cache.count++;
        cache.time = ++time;
        judge.insert(cache);
        it->second = cache;
        return cache.value;
    }
    
    void put(int key, int value) 
    {
        if(capacity == 0)
            return;
        auto it = table.find(key);
        if(it == table.end())
        {
            if(table.size() == capacity)
            {
                //先将不活跃的元素删除
                table.erase(judge.begin()->key);
                judge.erase(judge.begin());
            }
            Value put_(0, ++time, key, value);
            table.insert({key, put_});
            judge.insert(put_);
        }
        else
        {
            Value temp = it->second;
            judge.erase(temp);
            Value put_(++temp.count, ++time, key, value);
            it->second = put_;
            judge.insert(put_);
        }
    }

private:  
    const int capacity;
    int time;
    unordered_map<int, Value> table;
    set<Value> judge;
};

时间复杂度分析：因为set的底层是红黑树，所以插入删除操作都是O(logN)，上述LFU设计的数据结构在get和put时间复杂度也是O(logN)。

方法二：双哈希表+双向链表

思路和算法

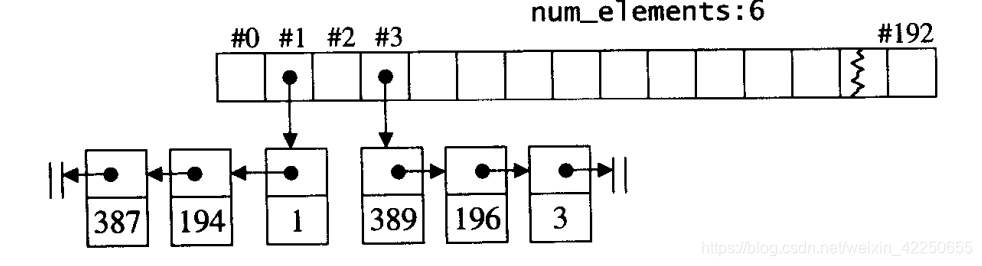
我们定义两个哈希表，第一个 freq_table 以频率 freq 为索引，每个索引存放一个双向链表，这个链表里存放所有使用频率为 freq 的缓存，缓存里存放三个信息，分别为键 key，值 value，以及使用频率 freq。第二个 iter_table 以键值 key 为索引，每个索引存放对应缓存在 freq_table 中链表里的内存地址，这样我们就能利用两个哈希表来使得两个操作的时间复杂度均为 O(1)O(1)。同时需要记录一个当前缓存最少使用的频率 minFreq，这是为了删除操作服务的。
对于 get(key) 操作，我们能通过索引 key 在 key_table 中找到缓存在 freq_table 中的链表的内存地址，如果不存在直接返回 -1，否则我们能获取到对应缓存的相关信息，这样我们就能知道缓存的键值还有使用频率，直接返回 key 对应的值即可。
但是我们注意到 get 操作后这个缓存的使用频率加一了，所以我们需要更新缓存在哈希表 freq_table 中的位置。已知这个缓存的键 key，值 value，以及使用频率 freq，那么该缓存应该存放到 freq_table 中 freq + 1 索引下的链表中。所以我们在当前链表中 O(1)O(1) 删除该缓存对应的节点，根据情况更新 minFreq 值，然后将其O(1)O(1) 插入到 freq + 1 索引下的链表头完成更新。这其中的操作复杂度均为 O(1)O(1)。你可能会疑惑更新的时候为什么是插入到链表头，这其实是为了保证缓存在当前链表中从链表头到链表尾的插入时间是有序的，为下面的删除操作服务。
对于 put(key, value) 操作，我们先通过索引 key在 iter_table 中查看是否有对应的缓存，如果有的话，其实操作等价于 get(key) 操作，唯一的区别就是我们需要将当前的缓存里的值更新为 value。如果没有的话，相当于是新加入的缓存，如果缓存已经到达容量，需要先删除最近最少使用的缓存，再进行插入。
先考虑插入，由于是新插入的，所以缓存的使用频率一定是 1，所以我们将缓存的信息插入到 freq_table 中 1 索引下的列表头即可，同时更新 iter_table[key] 的信息，以及更新 minFreq = 1。
那么剩下的就是删除操作了，由于我们实时维护了 minFreq，所以我们能够知道 freq_table 里目前最少使用频率的索引，同时因为我们保证了链表中从链表头到链表尾的插入时间是有序的，所以 freq_table[minFreq] 的链表中链表尾的节点即为使用频率最小且插入时间最早的节点，我们删除它同时根据情况更新 minFreq ，整个时间复杂度均为 O(1)O(1)。

class LFUCache
{
public:
    LFUCache(int capacity_) 
        : capacity(capacity_), 
          minfreq(0)    
    {
        iter_table.clear();
        freq_table.clear();
    }
    
    int get(int key) 
    {
        if(capacity == 0)
            return -1;
        auto it = iter_table.find(key);
        if(it == iter_table.end())
            return -1;
        list<Value>::iterator iter = it->second;
        //在此处一定要先存储iter的值，因为在下面删除list中的结点iter时会导致iter迭代器失效
        int value = iter->value;
        int freq = iter->freq;
        Value new_node(key, value, freq +1);
        //删除iter->freq中key对应的元素,此处操作会导致迭代器iter失效
        freq_table[freq].erase(iter);
        if(freq_table[freq].size() == 0)
        {
            freq_table.erase(freq);
            if(minfreq == freq)
                minfreq += 1;
        }
        freq_table[freq+1].push_front(new_node);
        iter_table[key] = freq_table[freq+1].begin();
        return new_node.value;
    }
    
    void put(int key, int value) 
    {
        if(capacity == 0)
            return;
        auto it = iter_table.find(key);
        if(it == iter_table.end())
        {
            //元素已满
            if(iter_table.size() == capacity)
            {
                auto it2 = freq_table[minfreq].back();
                iter_table.erase(it2.key);
                freq_table[minfreq].pop_back();
                if(freq_table[minfreq].size() == 0)
                {
                    freq_table.erase(minfreq);
                }
            }
            freq_table[1].push_front(Value{key, value, 1});
            iter_table[key] = freq_table[1].begin();
            minfreq = 1;
        } 
        else
        {
            list<Value>::iterator iter = it->second;
            //创建新元素
            int freq = iter->freq;
            Value new_node(iter->key, value, freq +1);
            //将freq_table中iter->freq所对应的元素删除
            freq_table[iter->freq].erase(iter);
            //list中元素为空，则将该list删除
            if(freq_table[freq].size() == 0)
            {
                freq_table.erase(freq);
                if(minfreq == freq)
                    minfreq += 1;
            }
            freq_table[freq+1].push_front(new_node);
            iter_table[key] = freq_table[freq+1].begin();   
        }
    }
private:   
    struct Value
    {   
        Value(int key_, int value_, int freq_)
         : key(key_),
           value(value_),
           freq(freq_) {}
        int key;
        int value;
        int freq;
    };
    int capacity;
    int minfreq;
    unordered_map<int, list<Value>::iterator> iter_table;
    unordered_map<int, list<Value> > freq_table;
};

题目描述

解析

方法一 ：哈希表+平衡二叉树

方法二 ： 双哈希表+双向链表

方法一：哈希表+平衡二叉树

方法二：双哈希表+双向链表