二叉查找树
在正式介绍AVL树之前,我们先来了解一下二叉查找树.
二叉查找树（Binary Search Tree）（又称二叉搜索树，二叉排序树）,它或者是一棵空树，
或者是具有下列性质的二叉树：
若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉排序树。
那么二叉查找树的引入有什么用呢?
当我想要在查找某个数,如果是在二叉查找树中,我就不需要遍历整棵树了,我可以根据当前遍历到的结点的值来确定搜索方向,因为二叉搜索树的性质(左小右大),每一次的查找都会将范围缩小(如果是极度平衡的树那么每次会将范围缩小一半了),与二分搜索的思想类似.
那么,为什么又要引入平衡二叉树呢
二叉查找树的结构与值的插入顺序有关，同一组数，若其元素的插入顺序不同，二叉查找树的结构是千差万别的。
如果一组数是[3,2,1,4,5],它最后形成的树是这样的:
但是,如果是[1,2,3,4,5]呢?
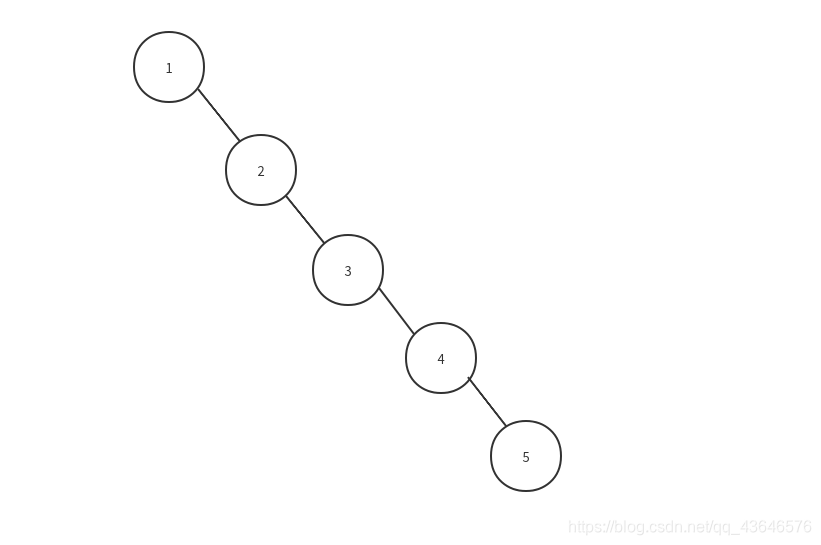
可以看出,上面的二叉查找树已经近似一个链表了,如果此时要查找5,时间复杂度就是O(n).
为了避免二叉查找树变成“链表”，这就引入了平衡二叉树，即让树的结构看起来尽量“均匀”，左右子树的节点数尽量一样多。
平衡二叉树
平衡二叉树，又称AVL树，它满足二叉查找树的所有性质,在此之上,左右子树的高度差最大为1.
AVL，则是取自两个发明平衡二叉树的科学家的名字：G. M. Adelson-Velsky和E. M. Landis。
平衡因子:该节点左子树高度减去右子树高度.
那么,同样给定一组数,怎样构造平衡二叉树呢?
先按照生成二叉查找树的方法构造二叉树，直至二叉树变得不平衡(左子树与右子树的高度差大于1)。
此时便需要对二叉树进行调整了,如何调整,就要看插入的导致二叉树不平衡的节点的位置。
主要有四种调整方式：LL（左旋）、RR（右旋）、LR（先左旋再右旋）、RL（先右旋再左旋）。
注:我这里的LL就是向左旋转(平衡因子 == -2),而网上大多数其他的博客都是LL向右旋转(平衡因子 == 2),其它三种旋转也是这种情况(代码意义都是一样的,只是在这理解不一样,具体可以看下面的详细解释).
这里先给出定义
template <typename T>
class AVLNode
{
public:
T key;
AVLNode<T> *left;
AVLNode<T> *right;
int height;
AVLNode(T value, AVLNode<T> *l, AVLNode<T> *r) : key(value), left(l), right(r), height(0) {
}
};
template <typename T>
class AVLTree
{
public:
AVLNode<T> *root;
AVLTree() : root(nullptr) {
}
~AVLTree();
//插入节点
void Insert(AVLNode<T> *&root, T );
//删除节点
bool Delete(AVLNode<T> *&root, T );
//中序遍历
void InOrderTra(AVLNode<T> *root) const;
//最小值节点
AVLNode<T> *FindMin(AVLNode<T> *root) const;
//最大值节点
AVLNode<T> *FindMax(AVLNode<T> *root) const;
private:
//求树的高度
int GetHeight(AVLNode<T> *root);
//左旋
AVLNode<T> *LL(AVLNode<T> *root);
//右旋
AVLNode<T> *RR(AVLNode<T> *root);
//先左旋再右旋
AVLNode<T> *LR(AVLNode<T> *root);
//先右旋再左旋
AVLNode<T> *RL(AVLNode<T> *root);
//销毁AVLTree
void destory(AVLNode<T> *&root);
};
//在这里,空的二叉树的高度是0，非空树的高度等于它的最大层次(根的层次为1，根的子节点为第2层，依次类推)。
template <typename T>
int AVLTree<T>::GetHeight(AVLNode<T> *root)
{
if(root != nullptr)
return root->height;
return 0;
}
LL(左旋)
LL（左旋）就是向左旋转一次.
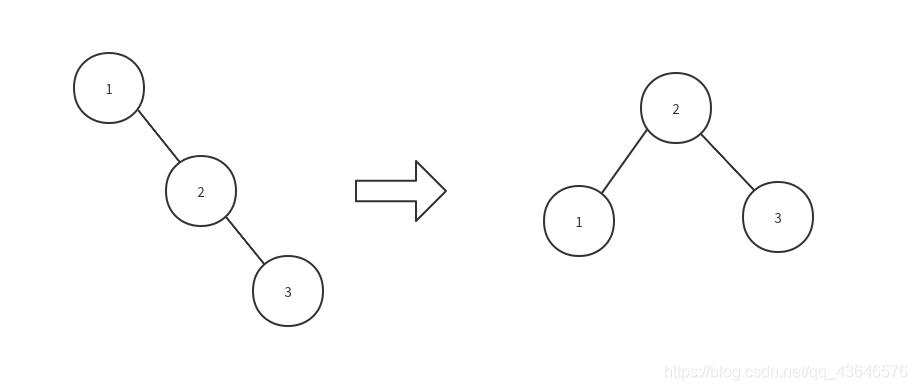最简洁的左旋
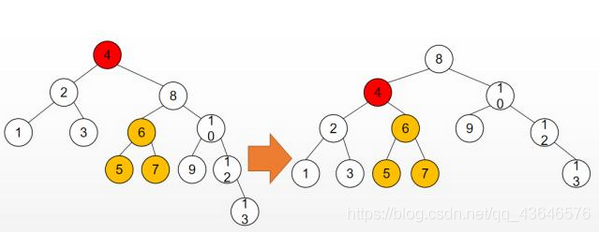
第一幅图是最简洁的左旋了,但更多时候往往不会这么简单,我们看第二幅图(插入13导致值为4的节点不平衡):
红色节点为插入后不平衡的节点，黄色部分为需要改变父节点的分支，左旋后，原红色节点的右孩子节点变成了根节点，
红色节点变成了它的左孩子，而它原本的左孩子（黄色部分）不能丢，而此时红色节点的右孩子是空的，于是就把黄色部分
放到了红色节点的右孩子的位置上.可以看出调整后二叉树就平衡了并且也符合左小右大的性质要求.
template <typename T>
AVLNode<T> * AVLTree<T>::LL(AVLNode<T> *root)
{
AVLNode<T> *q = root->right;
root->right = q->left;
q->left = root;
root->height = max(GetHeight(root->left), GetHeight(root->right)) + 1;
q->height = max(GetHeight(q->left), GetHeight(q->right)) + 1;
return q;
}
RR(右旋)
RR（右旋）就是向右旋转一次.
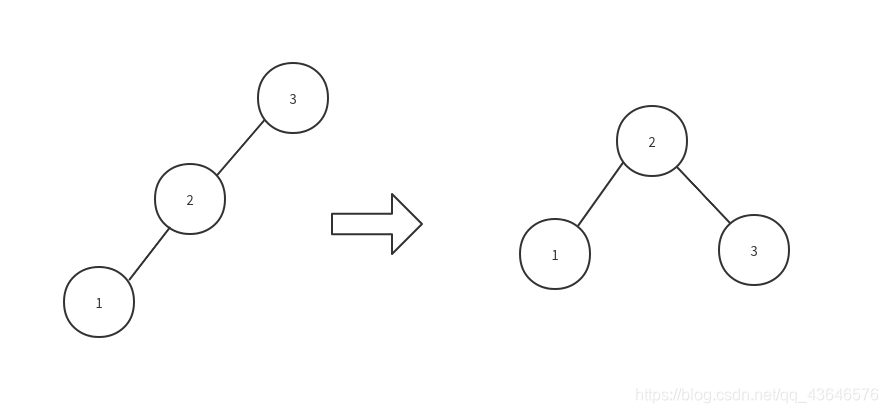最简洁的右旋
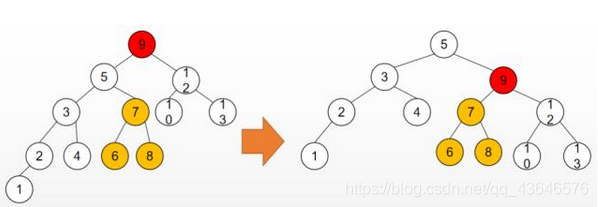
第一幅图是最简洁的右旋了,但更多时候往往不会这么简单,我们看第二幅图(插入1导致值为9的节点不平衡):
红色节点为插入后不平衡的节点，黄色部分为需要改变父节点的分支，右旋后，原红色节点的左孩子节点变成了根节点，
红色节点变成了它的右孩子，而它原本的右孩子（黄色部分）不能丢，而此时红色节点的左孩子是空的，于是就把黄色部分
放到了红色节点的左孩子的位置上。
template <typename T>
AVLNode<T>* AVLTree<T>::RR(AVLNode<T> *root)
{
AVLNode<T> *q = root->left;
root->left = q->right;
q->right = root;
root->height = max(GetHeight(root->left), GetHeight(root->right)) + 1;
q->height = max(GetHeight(q->left), GetHeight(q->right)) + 1;
return q;
}
LR（先左旋再右旋）
LR（先左旋再右旋）就是先将左子树左旋，再整体右旋.
最简洁的LR旋转
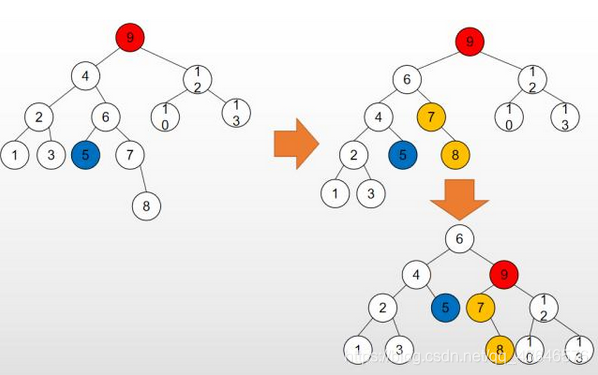
第一幅图是最简洁的LR旋转了,但更多时候往往不会这么简单,我们看第二幅图(插入8导致值为9的节点不平衡):
先将红色节点的左子树左旋，红色节点的左子树的根原本是值为4的节点，左旋后变为值为6的节点，
原来的根节点变成了左旋后根节点的左孩子，左旋后根节点原本的左孩子（蓝色节点）变成了原来的根节点的右孩子；
再整体右旋，原来的根节点（红色节点）变成了右旋后的根节点的右孩子，右旋后的根节点原本的右孩子（黄色节点）
变成了原来的根节点（红色节点）的左孩子。
这种情况我们只需要将LL(左旋)与RR(右旋)结合使用即可
template <typename T>
AVLNode<T>* AVLTree<T>::LR(AVLNode<T> *root)
{
root->left = LL(root->left);
return RR(root);
}
RL（先右旋再左旋）
RL（先右旋再左旋）就是先将右子树右旋，再整体左旋.
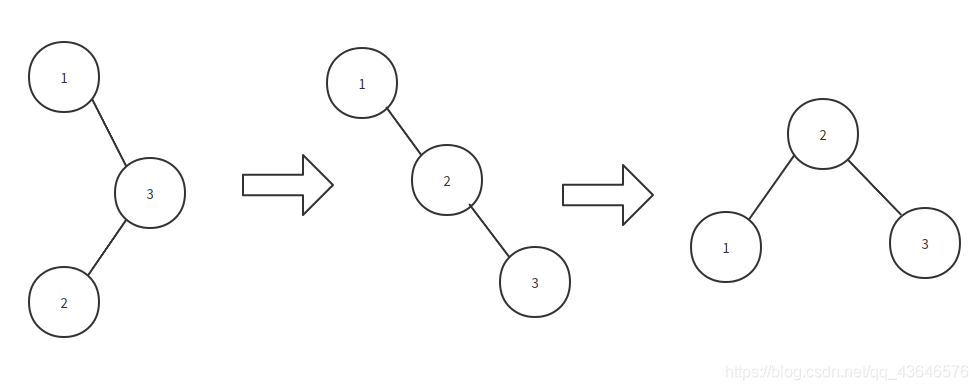
最简洁的RL旋转
将RR(右旋)与LL(左旋)结合使用即可
template <typename T>
AVLNode<T>* AVLTree<T>::RL(AVLNode<T> *root)
{
root->right = RR(root->right);
return LL(root);
}
平衡二叉树的构造
我们已经学习了四种调整方法,那么构造平衡二叉树就简单了,因为这就是边插入边调整的一个过程.
出现不平衡时到底是执行哪一种旋转，取决于插入的位置.
插入到不平衡节点的右子树的右子树上，自然是要执行LL旋转；
插入到不平衡节点的左子树的左子树上，自然是要执行RR旋转；
插入到不平衡节点的左子树的右子树上，自然是要执行LR旋转；
插入到不平衡节点的右子树的左子树上，自然是要执行RL旋转.
template <typename T>
void AVLTree<T>::Insert(AVLNode<T> *&root, T key)
{
if(root == nullptr)
root = new AVLNode<T>(key, nullptr, nullptr);
else if(key < root->key) //插入到左子树中
{
Insert(root->left, key);
//判断平衡情况
if(GetHeight(root->left) - GetHeight(root->right) == 2)
{
//左子树的左子树
if(key < root->left->key)
root = RR(root);
//左子树的右子树
else
root = LR(root);
}
}
else if(key > root->key) //插入到右子树中
{
Insert(root->right, key);
//判断平衡情况
if(GetHeight(root->right) - GetHeight(root->left) == 2)
{
//右子树的右子树
if(key > root->right->key)
root = LL(root);
//右子树的左子树
else
root = RL(root);
}
}
else
cout << "添加失败！" << endl;
//更新高度
root->height = max(GetHeight(root->left), GetHeight(root->right)) + 1;
}