下面是字符串匹配问题的一个例子
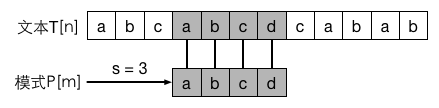
如果p在文本T中出现,那么称s是有效偏移,否则为无效偏移。下面介绍字符串匹配的算法
朴素算法:
该算法通过一个循环找到所有有效偏移,该循环对n-m-1个可能的s值进行检测,然后一一判断。
时间复杂度为O((n-m+1)m)
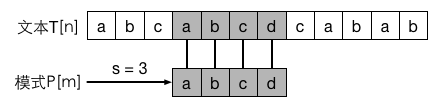
伪代码:
n = T.length
m = P.length
for s = 0 to n-m
if P[1..m] == T[s+1..s+m]
print("%d", s);
朴素算法的效率并不高,一是因为如果匹配失败,则文本串和模式串都要回头重新开始下一轮匹配,并没有保存所匹配到的
信息。然而这些信息非常有用。二是当其他s无效时,他也只关心一个有效的s值。
kmp算法:
kmp算法与朴素算法相比,派出了当匹配失败时文本串的回溯,而是利用已经得到的部分匹配结果,将模式串向右滑动尽可能
远的距离后,再进行比较。这样改进后的时间复杂度为O(m+n).
kmp算法的核心就是每次匹配失败后,模式串的滑动距离,我们用next数组来记录每个字符的值,下面分析模式串为
abaabcac的next数组。公式如下:
abaabcac的next数组求解:
1.当j = 1时,由定义得,next[1]=0。
2.当j=2时满足I<kj的k值不存在.由定义得知next[2]=1.
3.当j=3时,由于 T2≠T1,且next[1]=0,则next[3]=1.
4.当j=4时 由于T3=4,则next[4]=nex[3]+1, nexl[4]=2.
5.当j=5时,由于T4≠T2,且next[2]的值是1,故继续比较T4和T1,由于T4=T1,.则net[5]=next[2]+1,即next[5]=2.
6.当j=6时由于T5=T2,则next[6]=next[5]+1,即next[6]=3.
7.当j=7时,由于T6≠T3,且next[3]的值是1,故继续比较T6和T1,由于T6≠T1,且next[1]=0,则next[7]=1.
next数组求法:
int j = 1, k = 0;
next[1] = 0;
while ( j < T.len ) {
if ( k == 0 || T.ch[j] == T.ch[k] ) {
++j;
++k;
next[j] = l;
}
else
k = next[k];
}
kmp模式匹配算法
int i = p, j = 1; //文本串从p开始
while ( i <= S.len && j <= T.len ) {
if ( j == 0 || S.ch[i] == T.ch[j] ) {
++i;
++j;
}
else
j = next[j]; //模式串右滑
if ( j > T.;en )
return i - T.len;
else
return 0;
}
上述next数组尚存在缺陷。假设文本串为“aaabaaaab”模式串为“aaaab”,则next数组依次为0 1 2 3 4.当i =4、j =4时,匹配失败,模式串右滑,还要进行i=4,j=3;i=4,j=2;i=4,j=1这三次多余的比较,因为模式串前四个字符全部相同。因此,只需要直接进行i=5,j=1的比较。
通过分析之后,计算j个字符的nextval值时,要看j字符是否和第j个字符的nextval值指向的字符相等。若相等,则nextval[j] = nextval[next[j]];负责,nextval[j] = next[j].
由上述得出结果:
j 1 2 3 4 5
模式串 a a a a b
next[j] 0 1 2 3 4
nextval[j] 0 0 0 0 4
nextval[]:
int j = 2, k = 0;
Get_next(T, next); //获得next[]的值
nextval[1] = 0;
while ( j <= T.len ) {
k = next[j];
if ( T.ch[j] == T.ch[k] )
nextval[j] = nextval[k];
else
nextval[j] = next[j];
j++;
}
