分治法
思想:将原问题分解为几个规模较小但类似于原问题的子问题,递归地求解这些子问题,然后再合并这些子问题的解来建立原问题的解。
分治法在每层递归中都有三个步骤:
分解:将原问题分为若干个子问题,这些子问题是原问题的规模较小的实例。
解决:这些子问题,递归地求解各个子问题。若子问题的规模足够小,则直接求解。
合并:这些子问题的解成原问题的解。
分治法之快速排序(随机抽样优化算法)
核心代码:
int partition ( int a[], int p, int r )
{
int i, j;
i = p-1;
for ( j = p; j <= r-1; j++ ) {
if ( a[j] <= a[r] ) {
i++;
swap(i, j); //swap函数要自己写
}
}
swap(i+1, r);
return i+1;
}
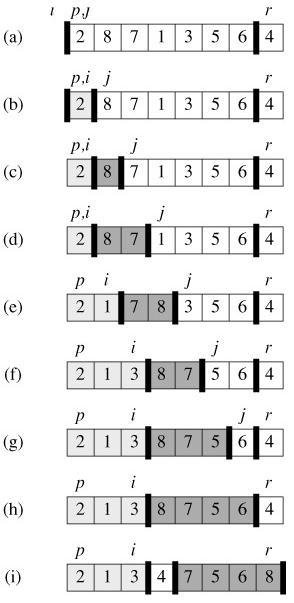
完整代码:
#include<stdio.h>
int a[101];
void swap ( int x, int y )
{
int t;
t = a[x];
a[x] = a[y];
a[y] = t;
return;
}
int partition ( int a[], int p, int r )
{
int i, j;
i = p-1;
for ( j = p; j <= r-1; j++ ) {
if ( a[j] <= a[r] ) {
i++;
swap(i, j);
}
}
swap(i+1, r);
return i+1;
}
int random_partition ( int a[], int p, int r )
{
int i;
i = rand() % (r - p + 1) + p; //随机选择数组中一个数和最后一个交换,这样保证啊a[r]是等概率地从子数组中选取的
swap(r, i);
return partition(a, p, r);
}
void random_quicksort ( int a[], int p, int r )
{
int q;
if ( p < r ) {
q = random_partition(a, p, r); //将问题分为几个子问题
random_quicksort(a, p, q-1); //运用递归法调用自己实现分治
random_quicksort(a, q+1, r);
}
}
int main (void)
{
int n, i;
scanf("%d", &n);
for ( i = 1; i <= n; i++ ) {
scanf("%d", &a[i]);
}
random_quicksort(a, 1, n);
for ( i = 1; i <= n; i++ ) {
printf("%d ", a[i]);
}
return 0;
}
分治法之归并排序
核心代码:
void Merge ( int a[], int p, int q, int r )
{
int n1, n2, i, j, k;
n1 = q-p+1;
n2 = r-q;
for ( i = 1; i <= n1; i++ )
L[i] = a[p+i-1];
for ( j = 1; j <= n2; j++ )
R[j] = a[q+j];
L[n1+1] = INT_MAX;
R[n2+1] = INT_MAX;
i = 1;
j = 1;
for ( k = p; k <= r; k++ ) {
if ( L[i] <= R[j] ) {
a[k] = L[i++];
}
else {
a[k] = R[j++];
}
}
}
核心代码图解
归并排序过程图解
完整代码:
#include<stdio.h>
#include <limits.h>
int a[100], L[100], R[100];
void Merge ( int a[], int p, int q, int r )
{
int n1, n2, i, j, k;
n1 = q-p+1;
n2 = r-q;
for ( i = 1; i <= n1; i++ )
L[i] = a[p+i-1];
for ( j = 1; j <= n2; j++ )
R[j] = a[q+j];
L[n1+1] = INT_MAX;
R[n2+1] = INT_MAX;
i = 1;
j = 1;
for ( k = p; k <= r; k++ ) {
if ( L[i] <= R[j] ) {
a[k] = L[i++];
}
else {
a[k] = R[j++];
}
}
}
void mergesort ( int a[], int p, int r )
{
int q;
if ( p < r ) {
q = (p+r)/2; //分解待排序的n个元素的序列成具n/2个元素的子序列
mergesort(a, p, q); //使用归并排序递归地排序两个子序列
mergesort(a, q+1, r);
Merge(a, p, q, r); //合并两个已排序的子序列以产生已排序的答案
}
else
return;
}
int main (void)
{
int n, i;
scanf("%d", &n);
for ( i = 1; i <= n; i++ ) {
scanf("%d", &a[i]);
}
mergesort(a, 1, n);
for ( i = 1; i <= n; i++ ) {
printf("%d ", a[i]);
}
return 0;
}
最后再说一点,快速排序属于不稳定排序,而归并排序属于稳定排序。



