前缀树
前缀树又称字典树,其中的键通常是字符串.键不是直接保存在结点中,而是由结点在树中的位置决定.
一个结点的所有子孙都有相同的前缀,也就是这个结点对应的字符串.而一般根节点是对应空字符串.
前缀数的特点:
1:根节点不包含字符,除根节点外的每一个子节点都包含一个字符。
2:从根节点到某一节点,路径上经过的字符连接起来,就是该节点对应的字符串。
3:每个单词的公共前缀作为一个字符节点保存。
例如一个集合为{a,to,tea,ted,ten,i,in,inn}; 用前缀数表示为
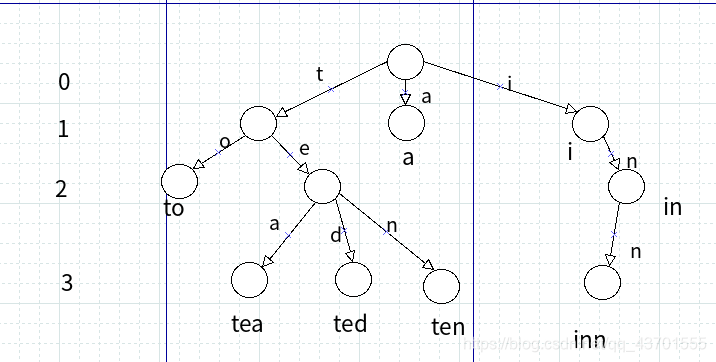
每个单词的结束对应一个单词结点.
从根节点到每个单词结点的路径上所有字母裂解而成的字符串就是该节点对应的字符串.
如何用代码实现呢?
假设所有字母均为小写字母,则最多只有 26 个
假设最长的单词不超过 100 个字母.
然后用二维数组存储
const int sigma_size = 26;
const int maxn = 100 + 10;
ch[maxn][sigma_size]
首先考虑插入,怎样讲一个字符串插入到 trie树 中.
可以将 根结点 变为 ch[0] ,则 ch[0][sigma_size] 代表 第一层中的 26 个结点(最多)
将 第一层 变为 ch[1],则 ch[1][sigma_size] 代表第二层中的 26 个结点(最多)
…
插入时,将一个字符串分解为单个字母,每层放置一个字母,直到将所有字母全部插入到 trie树中.
然后,用 val[maxn] 数组保存 某一个字符串前缀出现的次数.
那么怎样利用 val数组呢?
因为刚开始的时候,树为空,并且我们插入的时候是有先后顺序的,所以我们可以利用字符串插入的顺序来利用 val数组.
例如, 插入三个字符串 {a,to,tea}.
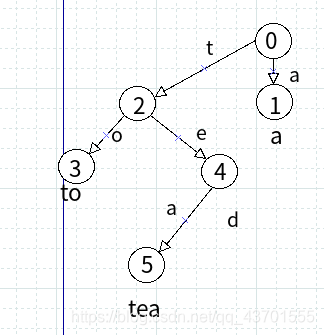
则 val[1] 代表 a 出现的次数
val[2] 代表 t 出现的次数
val[3] 代表 to 出现的次数
val[4] 代表 te 出现的次数
…
代码实现:
u 开始代表 根结点.
sz 代表创建的第几个结点
void insert(string s)
{
int u = 0,n = s.size();
for(int i = 0;i < n;i++)
{
int c = s[i] - 'a';
if(!ch[u][c]) //结点不存在
{
ch[u][c] = sz++;
}
val[ch[u][c]]++; //出现次数 + 1
u = ch[u][c]; //往下走一层
}
}
然后是查询(和插入类似)
int search(string s)
{
int u = 0,n = s.size();
for(int i = 0;i < n;i++)
{
int c = s[i] - 'a';
if(!ch[u][c]) return 0; //结点不存在
u = ch[u][c]; //往下走
}
return val[u]; //返回该字符串出现的次数
}