二叉树的公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
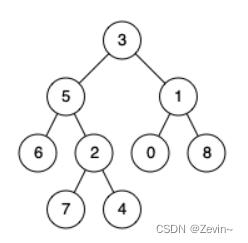
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
保存路径法
记录从根到对应节点的路径,找到最近公共节点
class Solution {
public:
bool findpath(stack<TreeNode*>& con,TreeNode* root,TreeNode* x)
{
if(root==nullptr)
return false;//走到空,没找到
con.push(root);//先入栈再说
if(root==x)
return true;
if(findpath(con,root->left,x))//如果在左边找到了,就不要往右边去找
{
return true;
}
if(findpath(con,root->right,x))//如果在右边找到了,就别要去左边找了
return true;
//左边也没找到,就要出栈
con.pop();
return false;//往上面走告知在左边没找到
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
//方法2,记录路劲,使用栈,从根到底部的路劲
stack<TreeNode*> pstack;
stack<TreeNode*> qstack;
findpath(pstack,root,p);
findpath(qstack,root,q);
int diff=pstack.size()-qstack.size();//两者的差值
if(diff<0)
diff=-diff;
bool plarger=pstack.size()>qstack.size();
bool qlarger=!plarger;
while(diff--)//把两个减到一样多
{
if(plarger)
pstack.pop();
else if(qlarger)
qstack.pop();
}
while(!pstack.empty())
{
if(pstack.top()==qstack.top())//直到找到就返回
return pstack.top();
else
{
pstack.pop();
qstack.pop();
}
}
return nullptr;
}
};
查找节点法
如果要找的节点在左右两边,那么我就是节点,如果都在左边,就去左边找,如果都在右边,就去右边找
class Solution {
public:
bool find(TreeNode* root,TreeNode* x)//查找一个节点
{
if(root==nullptr)//走到空,就没找到
return false;
if(root==x)//为x就找到了
return true;
return find(root->left,x)||find(root->right,x);//没找到就去左边或右边找,找到了就为真
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
//分别求出两个的路径
//用栈来存储路径
if(root==nullptr)//为空就没找到
return nullptr;
if(root==p||root==q)
return root;//其中一个就是要找的,那就是
bool pinleft=find(root->left,p);
bool pinright=!pinleft;
bool qinleft=find(root->left,q);
bool qinright=!qinleft;
if((pinleft&&qinright)||(pinright&&qinleft))//在左右两边,那就是它了
return root;
else if(pinleft&&qinleft)//都在左边,就去左边递归的找
return lowestCommonAncestor(root->left,p,q);
else if(pinright&&qinright)//都在右边,就去右边递归的找
return lowestCommonAncestor(root->right,p,q);
return nullptr;
}
};