目录
矩阵力扣题讲解
二进制二维数组image水平反转在取反
int** flipAndInvertImage(int** image, int imageSize, int* imageColSize, int* returnSize, int** returnColumnSizes){
int i, j, col;
int **ret = (int **)malloc( sizeof(int *) * imageSize ); // (1)
*returnColumnSizes = (int *)malloc( sizeof(int) * imageSize ); // (2)
for(i = 0; i < imageSize; ++i) {
col = imageColSize[i]; // (3)
ret[i] = (int *)malloc( sizeof(int) * col ); // (4)
(*returnColumnSizes)[i] = col; // (5)
for(j = 0; j < col; ++j) {
ret[i][j] = 1 - image[i][ col-1-j ]; // (6)
}
}
*returnSize = imageSize; // (7)
return ret; // (8)
}
image是传过来二维数组,
imagesize是传过来的二维数组的行数,
imagecolsize是传过来二维数组每行的列数
returnSize是传回去二维数组的行数
returnColumnSizes是传回去二维数组每行的列数
返回的时候要malloc一个二维数组来接收
同时每行也要malloc处每行的元素个数(最后malloc完二维数组后,就对每个一维数组进行malloc)
1.最富有客户的资产总量
给你一个
m x n的整数网格accounts,其中accounts[i][j]是第i位客户在第j家银行托管的资产数量。返回最富有客户所拥有的 资产总量 。客户的 资产总量 就是他们在各家银行托管的资产数量之和。最富有客户就是 资产总量 最大的客户。
示例 1:
输入:accounts = [[1,2,3],[3,2,1]] 输出:6 解释:第 1 位客户的资产总量 = 1 + 2 + 3 = 6 第 2 位客户的资产总量 = 3 + 2 + 1 = 6两位客户都是最富有的,资产总量都是 6 ,所以返回 6 。示例 2:
输入:accounts = [[1,5],[7,3],[3,5]] 输出:10 解释:第 1 位客户的资产总量= 6第 2 位客户的资产总量= 10第 3 位客户的资产总量= 8 第 2 位客户是最富有的,资产总量是 10示例 3:
输入:accounts = [[2,8,7],[7,1,3],[1,9,5]] 输出:17
思路:求出每行的和,再将每行和进行比较,求出最大值进行返回
int maximumWealth(int** accounts, int accountsSize, int* accountsColSize){
int i,j,col;
int arr[accountsSize];//用一个arr数组来接收每行和
memset(arr,0,accountsSize*sizeof(int));同时要对他初始化为0
int max;//定义max为最终最大返回值
for(i=0;i<accountsSize;i++)
{
for(j=0;j<accountsColSize[i];j++)
{
arr[i]+=accounts[i][j];
}
}
max=arr[0];//max赋初值第一个元素
for(i=0;i<accountsSize;i++)
{
if(max<arr[i])
{
max=arr[i];
}
}
return max;
}转置矩阵
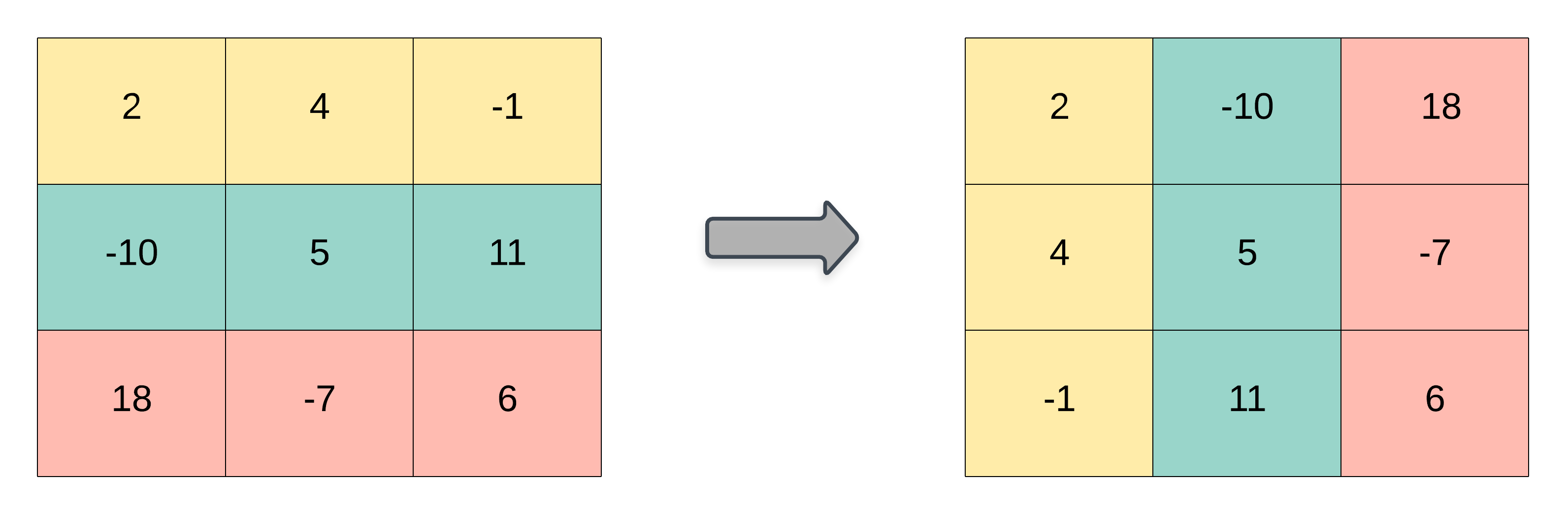
给你一个二维整数数组
matrix, 返回matrix的 转置矩阵 。矩阵的 转置 是指将矩阵的主对角线翻转,交换矩阵的行索引与列索引。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[1,4,7],[2,5,8],[3,6,9]]示例 2:
输入:matrix = [[1,2,3],[4,5,6]] 输出:[[1,4],[2,5],[3,6]]
思路:对角线互换,行变列,列变行
1.returnsize返回的是转置后返回的二维数组的行数;
2.*returnColumnSizes是返回的二维数组的每行的列数
3.返回的二维数组必须自己malloc出来,同时返回的二维数组每一行的元素也要自己malloc出来,
/**
* Return an array of arrays of size *returnSize.
* The sizes of the arrays are returned as *returnColumnSizes array.
* Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
*/
int** transpose(int** matrix, int matrixSize, int* matrixColSize, int* returnSize, int** returnColumnSizes)
{
int i,j,col;
col=matrixColSize[0];//
int **ret=(int **)malloc(sizeof(int*)*col); //ret的行数是matrix的列数
*returnColumnSizes=(int*)malloc(sizeof(int)*col);//*returnColumnSize返回的每行的个数是原二维数组的列数
*returnSize=col; //返回的行数是原来的列数
for(i=0;i<col;i++)
{
(*returnColumnSizes)[i]=matrixSize;//返回每行的列数是原来的行数
ret[i]=(int *)malloc(sizeof(int)*matrixSize);
}
for(i=0;i<matrixSize;i++)
{
for(j=0;j<col;j++)
{
ret[j][i]=matrix[i][j];
}
}
return ret;
}旋转图像
给定一个 n × n 的二维矩阵
matrix表示一个图像。请你将图像顺时针旋转 90 度。你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[7,4,1],[8,5,2],[9,6,3]]示例 2:
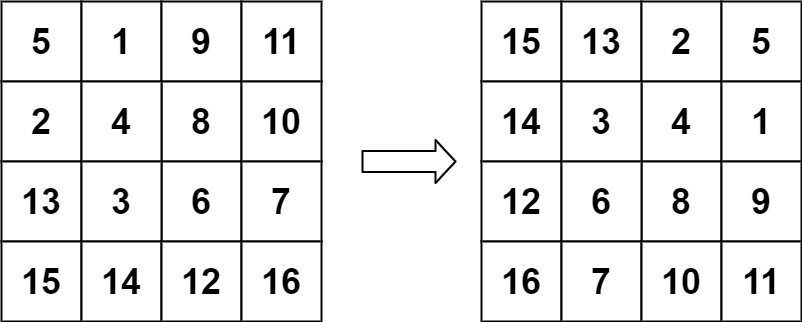
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]示例 3:
输入:matrix = [[1]] 输出:[[1]]示例 4:
输入:matrix = [[1,2],[3,4]] 输出:[[3,1],[4,2]]
void rotate(int** matrix, int matrixSize, int* matrixColSize){
int i=0;
int j=0;
int col;
int arr[matrixSize][matrixSize];//开辟一个arr二维数组,长度是matrixsize
for(i=0;i<matrixSize;i++)
{
col=matrixColSize[i]; //col是每行的列数
for(j=0;j<col;j++)
{
arr[j][col-1-i]=matrix[i][j];//因为是对matrix的i和j的遍历,所以matrix是[i][j],
arr是规律是arr[j][col-1-i]
}
}
for(i=0;i<matrixSize;i++)
{
col=matrixColSize[i];
for(j=0;j<col;j++)
{
matrix[i][j]=arr[i][j];//arr是已经旋转之后的数组,同时因为要旋转,所以要对原来的数组进行改变,把arr赋给matrix
}
}
return matrix;
}回旋矩阵
int main()
{
int i, j;
int m = 3;
int n = 3;
int ret[10][10];
memset(ret, 0, sizeof(ret));用memset内存函数对ret初始化为0
int count = 1;
for (i = 0; i < n / 2; i++)
{
//向右
for (j = i; j < m - i; j++)
{
ret[i][j] = count++;
}
//向下
for (j = i + 1; j < n - i; j++)
{
ret[j][m - 1 - i] = count++;
}
for (j = m - 2 - i; j >= i; j--)
{
ret[n - 1 - i][j] = count++;
}
for (j = n - 2 - i; j > i; j--)
{
ret[j][i] = count++;
}
if (n % 2 == 1)//假如n是奇数的话,中间还要填一个数
{
ret[n / 2][m / 2] = n * m;
}
}
for (i = 0; i < n; i++)
{
for (j = 0; j < m; j++)
{
printf("%d ", ret[i][j]);
}
printf("\n");
}