在操作系统的数据库中,使用驱逐算法来实现内存和磁盘之间的交互。当内存空间已满且需要将磁盘上的页面添加到内存中时,就需要将内存中的一个页面换出,以保证内存空间不会溢出。我们希望尽可能多地访问内存中的页面。
LRU算法
LRU算法(最近最少使用)是一种常用的驱逐算法,其工作原理如下:
- 每次插入数据时都将其添加到缓存的
头部。 - 当缓存已满需要删除数据时,删除缓存的
尾部数据,即最久未被访问的数据。 - 双端队列中不允许存在重复的数据。当插入的数据已经存在时,需要先将其删除,然后再将其添加到头部。
以下是LRU算法示意图:
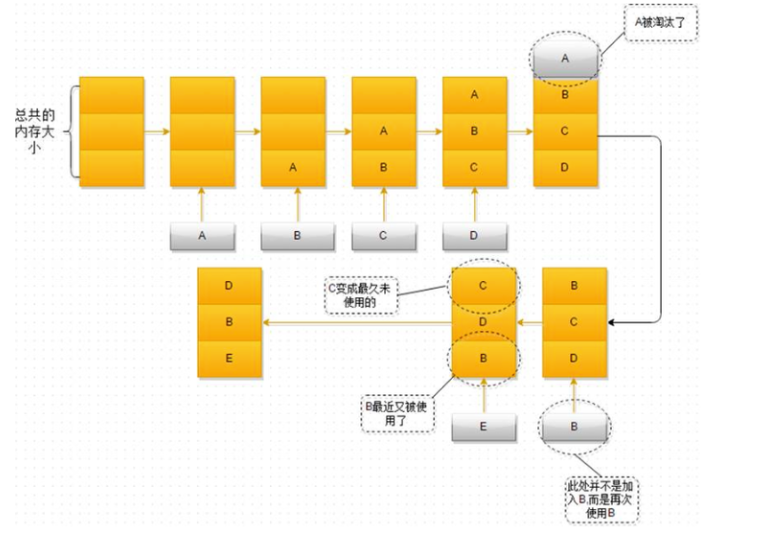
实现
使用一个双向链表来实现头插尾删,并通过哈希表来进行缓存的访问
#include <iostream>
using namespace std;
#include <unordered_map>
// LRU的节点
struct DListNode
{
int key_;
int value_;
DListNode *prev_;
DListNode *next_;
DListNode()
: key_(0), value_(0), prev_(nullptr), next_(nullptr) {
}
DListNode(int key, int value)
: key_(key), value_(value), prev_(nullptr), next_(nullptr)
{
}
};
//我们需要一个哈希表(判断当前是否有该节点)
//需要链表来存储数据
// lru容量
class LRU
{
public:
LRU(int capacity)
: capcity_(capacity), size_(0)
{
head_=new DListNode();
tail_=new DListNode();
head_->next_=tail_;
tail_->prev_=head_;
}
//访问某一个元素
int get(int key)
{
if(cache_.find(key)==cache_.end())
{
//没找到,直接返回
return -1;
}
//找到了,就拿到哈希表中对应的数据,就先删除后插入,把该节点放入到头部
DListNode* node=cache_[key];
move_to_head(node);
return node->value_;
}
//插入某个元素
//先查看当前插入的这个节点是否存在,如果存在,就需要拿到node,并且更新value,并且放到头部
//如果不存在,就插入到头部,如果size等于capacity,就需要删除尾部节点,再插入新的节点
void put(int key,int value)
{
//先查看当前节点是否存在
if(cache_.find(key)!=cache_.end())
{
//当前节点存在
//获得该节点,并且更新他的数据,在插入到头部
DListNode* node=cache_[key];
node->value_=value;//修改他的数据
move_to_head(node);//移动到头部
}
else{
//这里就是没有找到该元素
DListNode* node=new DListNode(key,value);
cache_[key]=node;
add_to_head(node);//插入到头部
size_++;
//超出了容量大小,就需要执行删除操作
if(size_>capcity_)
{
DListNode* target=remove_tail();
cache_.erase(target->key_);//删除该元素在cache中
delete(target);
size_--;
}
}
}
private:
unordered_map<int, DListNode *> cache_; //用来供访问的缓存
//我们每次就处理两个节点,一个头部插入,和尾巴删除
DListNode *head_; //存储链表的头节点,哨兵位
DListNode *tail_; //存储链表的尾节点的下一个节点,tail->prev代表的就是链表的尾节点
int size_; //当前LRU中的元素数量
int capcity_; //能够存储的最大容量
void remove_node(DListNode* node)//移除某个元素
{
//删除节点
node->prev_->next_=node->next_;
node->next_->prev_=node->prev_;
}
void add_to_head(DListNode* node)//把该数据放到头部
{
node->next_=head_->next_;
head_->next_->prev_=node;
head_->next_=node;
node->prev_=head_;
}
//把某一个刚访问过的节点,放到头部
void move_to_head(DListNode* node)
{
remove_node(node);//删除该节点
add_to_head(node);//添加到头部
}
//删除尾部元素
DListNode* remove_tail()
{
DListNode* target=tail_->prev_;//最后一个有效节点
remove_node(target);//移除该节点
return target;
}
};
特点
缺点
- 数据的使用情况需要额外的空间进行存储
- 会删除热点key,导致最希望命中的数据丢失
时钟置换算法(CLOCK Algorithm)
时钟置换算法使用一个指针周期性地指向缓冲区中的下一个页面。
当页面被访问时:
- 如果页面在缓冲区中,将其标记为最近使用
- 否则,发生缺页异常,替换指针指向的页面
替换选择规则:
- 选择尚未使用的页面作为替换受害者
- 优先选择未修改过的页面
对新页面:
- 标记为最近使用
- 设置为修改状态
将页指针移动到下一个页面。
设置页面为未使用状态的目的是:
- 持续选出未使用的页面替换
- 使页面进入活跃和不活跃周期
优点:
- 算法简单,需要很少的状态信息
- 通过周期性地访问每个页面,实现了类似时间分片的公平性
缺点:
- 无法考虑页面使用频率的不同
- 整体上,时钟算法充分利用了页面使用序列中的局部性,但不能很好地处理全局性。
时钟算法在处理页面替换的时候,更加注重最近被访问的页面,即局部性,他通过周期性的访问每个页面,使最近被访问的页面流在缓冲区中,这种局部性处理方式对于局部性较强的场景非常有效
时钟算法只是检查页面最近是否被访问来进行替换,无法考虑页面的使用频率和其他全局性特征,
这样删除了REF和m标记,直接描述主要流程。页指针hand泛指缓冲区中的下一个页面,默认未使用。
当页面最近使用时便标记为最近使用,其他未使用的页面仍然可以被替换。
由于在实际系统使用中页面不仅会被访问还会被修改,所以改进型Clock算法就是把页面分成四种情况:
- 最近既没修改也没访问
- 最近没访问但修改了
- 最近访问了但没修改
- 最近即访问又修改了
按照类似简单Clock算法(使用两个标号)来依次判断有没有情况1的页面,如果有就换出,如果没有就判断有没有情况2的页面,注意,当判断完后还是没有并不是去判断情况3和4,而是把所有访问标号都重置为0,再依次判断1和2,这样就能找到最适合换出的页面。
实现
struct Page {
bool is_exist_;//该页面是否存在
bool is_REF;//该页面是否被访问过
bool is_MODIFIED;//该页面是否被修改过
int pageid_;
Page(int pageid)
: pageid_(pageid), is_exist_(true), is_REF(true), is_MODIFIED(true) {
}
};
class CLOCK {
private:
list<Page> pages_;
list<Page>::iterator hand_;//页面值换的时候,通过迭代器的方式来进行页面的插入和删除
int size_;
int capacity_;
public:
CLOCK(int capacity)
: size_(0), capacity_(capacity) {
pages_.reserve(capacity_);
hand_ = pages_.begin();//指向头节点的指针
}
void clock_dispatch() {
while (true) {
if (hand_->is_exist_) {
if (hand_->is_REF) {
hand_->is_REF = false;
} else if (hand_->is_MODIFIED) {
hand_->is_MODIFIED = false;
} else {
//既不存在也没有修改过,这个就是置换的高优先级别
hand_->is_exist_ = false;
return;
}
}
//节点往后移动
advance(hand_, 1);
if (hand_ == pages_.end())//走到尾巴,重新走到头部
hand_ = pages_.begin();
}
}
void put(int pageid) {
if (size_ == capacity_) {
//满了,就需要进行值换
clock_dispatch();//进行页面置换
//hand现在指向的位置就是需要插入置换的节点
*hand_ = Page(pageid);
} else {
pages_.emplace_back(pageid);//页面中插入一个元素
size_++;//添加一个元素
}
advance(hand_, 1);//hand往后走1位
if (hand_ == pages_.end())//如果走到最后,就需要转到头节点位置上
hand_ = pages_.begin();
}
};
LFU
(Least Frequently Used):最近最少使用算法
一个数据在一段事件很少被访问到,那么可以认为他将来被访问的可能性很小,因此当空间满了,最小频率访问的数据应该最先被淘汰
如图,当插入/访问D时候,会将D的频次进行更新,并且对链表的顺序进行重新排序,当插入为F的时候,此时容器已经满了,就需要将链表的尾节点进行删除(尾节点是访问频次最少的节点),并且将该新节点插入到尾节点上,这就完成了内存淘汰
原理
LFU将数据和数据的访问频次保存在一个容量有限的容器中,当访问一个数据时
- 该数据在容器中,则将该数据的访问频次加1
- 该数据不在容器中,则将该数据加入到容器中,且访问频次设置为1

使用一个双哈希表,一个用来记录freq的哈希表,key就是出现的频率,value就是出现这一频率元素的链表
使用一个哈希表来用作缓存来进行访问
实现
#include <iostream>
#include <unordered_map>
#include <list>
using namespace std;
class LFUCache
{
private:
int capacity_;
int minFrequency_;
unordered_map<int, pair<int, int>> cache_; // key->{value,frequency},查询的时候直接查询这个cache
unordered_map<int, list<int>::iterator> keyIter_;//每个key对应的元素在frequency中的list某个位置的迭代器
unordered_map<int, list<int>> frequency_; //哈希表->key是出现的频次,value就是一个链表里面出现这个频次的元素
public:
LFUCache(int capacity)
: capacity_(capacity), minFrequency_(0)
{
}
//访问某个key
int get(int key)
{
//
if (cache_.find(key) == cache_.end())
{
return -1; //没有找到就返回-1
}
//找到了
int value = cache_[key].first;
int& freq = cache_[key].second;
frequency_[freq].erase(keyIter_[key]); //从原来的链表上删除这个元素
//更新频率
freq++;
frequency_[freq].push_back(key); //插入到对应频次的链表上
keyIter_[key] = --frequency_[freq].end();//更新迭代器对应的list迭代器节点
if (frequency_[minFrequency_].empty())
{
minFrequency_++;
}
return value; //获得这个元素对应的value
}
void put(int key,int value)
{
//插入一个元素
if (capacity_ <= 0)
return;
int existingValue = get(key);//根据这个key获得它对应的value
if (existingValue != -1)
{
//这个元素存在,只需要更新他的值就行了
cache_[key].first =value;
return;
}
//当前的值不存在
if (cache_.size() >= capacity_)
{
int evictkey = frequency_[minFrequency_].front(); //获得最小的元素
cache_.erase(evictkey);
keyIter_.erase(evictkey);
frequency_[minFrequency_].pop_front(); //删除第一个元素
}
//添加进新的元素
cache_[key] = {
value, 1};
frequency_[1].push_back(key);//往出现1次的频率链表中添加元素
keyIter_[key] = --frequency_[1].end();
minFrequency_ = 1;//因为是新插入进来的元素,所以就需要将最小频率修改为1
}
};
特点
优点
- 一般情况下,LFU效率比LRU要高,可以避免周期性或者偶发性的操作导致,缓存命中率会高一些
缺点
-
复杂度较高:需要额外维护一个队列或者双向链表,复杂度较高
-
对新缓存不友好:新加入的缓存容易被清理掉(如果有新数据加入,这个数据可能就被缓存删除),即使可能被经常访问
-
缓存污染:一旦缓存的访问模式变化,访问记录的历史存量,会导致缓存污染,因为对时间不敏感,所以
LFU更加容易出现缓存污染之前保存的访问记录可能会导致缓存中的内容出现错误或者不准确的情况
如:假设您访问一个网站时,网站的一些内容被缓存在您的浏览器中,以便您下次访问时可以更快地加载。但是,如果网站的内容被更新了,但是您的浏览器仍然使用了旧的缓存内容,这就会导致缓存污染。因为您的浏览器中保存的缓存内容已经不再与网站的实际内容匹配,这可能会导致显示错误或不准确的信息。这些缓存的数据就没有用了
-
内存开销:需要对每个缓存数据中维护一个访问次数,内存成本较大
-
处理器开销:需要对访问次数进行排序,每次新增加的数据都有可能会对链表进行重新排序,会增加一定的处理器开销