LIS算法

经典LIS算法：导弹拦截

某国为了防御敌国的导弹袭击，开发出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭，并观测到导弹依次飞来的高度，请计算这套系统最多能拦截多少导弹。拦截来袭导弹时，必须按来袭导弹袭击的时间顺序，不允许先拦截后面的导弹，再拦截前面的导弹。
Input
输入有两行，
第一行，输入雷达捕捉到的敌国导弹的数量k（k<=25），
第二行，输入k个正整数，表示k枚导弹的高度，按来袭导弹的袭击时间顺序给出，以空格分隔。
Output
输出只有一行，包含一个整数，表示最多能拦截多少枚导弹。
Sample Input
8
300 207 155 300 299 170 158 65
Sample Output
6

#include <stdio.h>
#include <algorithm>
using namespace std;
int Max;
int a[30];
int dp[30];
int main()
{
	int n;
	scanf("%d",&n);

	int i = 0;
	for(i = 0;i<n;i++)
	{
		scanf("%d",&a[i]);
	}

	int j = 0;
	for(i = 0;i<n;i++)
	{
		dp[i] = 1;
		for(j = 0;j<i;j++)
		{
			if(a[i] <= a[j]) dp[i] = max(dp[j]+1,dp[i]);

		}
		Max = max(dp[i],Max);
	}

	printf("%d\n",Max);
	return 0;
}

这是一道经典的LIS算法，即求最大上升子串，这道题就是求个最大下降子串，道理是相通的，核心思想就是我们初始令每个串的长度都是1，然后从第二个开始，每次从头开始遍历到当前数字的前一个，选取其中符合条件的，最长的子串与当前串拼接。图示如下：

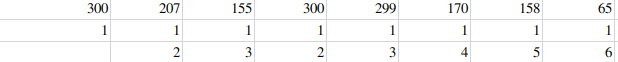
如果要打印最后的子串，只需要子串中每个数字保存下他的前一个数字的下标就可以了。