GroupBlog

题意

Description

现有一堆边长为1的已经放置好的积木，小明（对的，你没看错，的确是陪伴我们成长的那个小明）想知道当下雨天来时会有多少积水。小明又是如此地喜欢二次元，于是他把这个三维的现实问题简化成二维的问题。设雨量无穷、积木不透水、积木间无缝连接，问在这个二次元的世界里，已放置好的积木会有多少单位的积水量？
这里写图片描述

Input

第一行包含一个整数T(T≤100)，表示接下来的测试样例个数。每个测试样例有两行组成：第一行包含一个整数N(N≤1e6)，表示积木的列数；第二行包含N个整数Ai(Ai≤1e6)，表示第i列积木的个数。

Output

每个样例输出一行，包含一个整数，为题目所求。

Sample Input

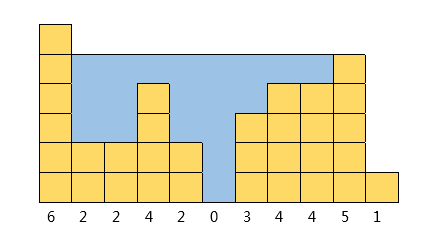
1
11
6 2 2 4 2 0 3 4 4 5 1

Sample Output

思路

数据范围是10^6，显然不能O(n^2)。
不自然的就想到了栈。
维护一个递减的栈。
如果，当前列比栈顶列低，那就入栈。
否则，就一直出栈，直至栈顶高于当前列。
理由是显然的，对于两个相对高些的列，它们之间的较低列显然是没用的。
最后，所有列都进行过后，对栈里元素依次出栈，并记录它们之间的矩形面积，再减去它们之间的方格总数，既是最终的答案。

代码

#include <stdio.h>
#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <algorithm>
#include <stack>

using namespace std;
#define LL long long

LL d[1000009], g[1000009];

int main()
{
    int T, n;
    scanf("%d", &T);
    while(T--)
    {
        scanf("%d", &n);
        for(int i=0; i<n; i++)
            scanf("%d", &d[i]);

        g[0] = d[0];
        for(int i=1; i<n; i++)
            g[i] = g[i-1] + d[i];
        stack<int> s;

        LL ans = 0;
        for(int i=0; i<n; i++)
        {
            if(s.empty())
            {
                s.push(i);
                continue;
            }
            int t;
            while(!s.empty())
            {
                t = s.top();
                if(d[t] > d[i])
                    break;
                s.pop();
            }

            if(s.empty())
                ans += (i-t-1)*d[t]-(g[i-1]-g[t]);

            s.push(i);
        }
        if(!s.empty())
        {
            int i = s.top();
            s.pop();
            while(!s.empty())
            {
                int t = s.top();
                s.pop();
                ans += (i-t-1)*d[i]-(g[i-1]-g[t]);
                i = t;
            }
        }
        printf("%lld\n", ans);
    }
    return 0;
}