之前做过类似的题,只是理解了,还没达到驾轻就熟,想到即敲出的地步,所以再练一次。
顺带将Manacher算法思想解释一遍,加强印象,也算作分享吧。
Manacher
我们用f(x)表示以x位置为中心的回文串的长度
j相对i的对应位置是j’
那么f(j)与f(j’)和f(i)有什么关系呢。
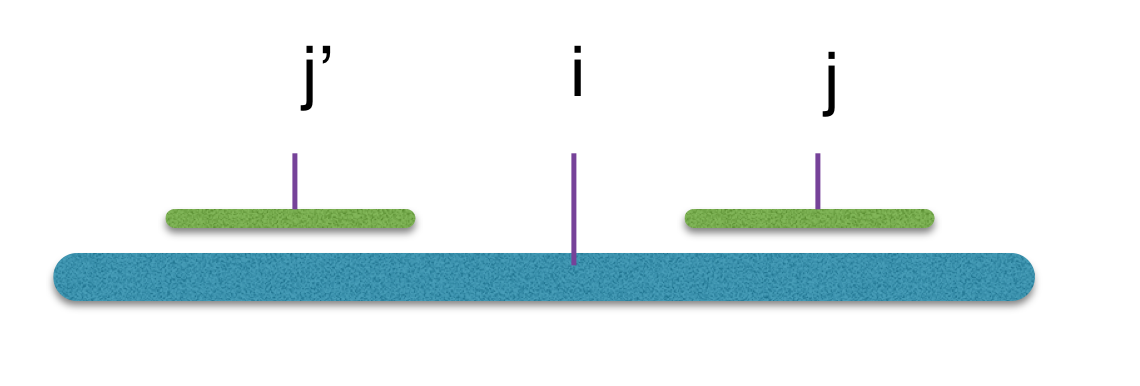
先看第一张图,下面那条横杠表示f(i),那么,既然j’与j相对应,j’的回文串长度已经求出,那么j位置的回文串长度一定是大于等于j’长度的。
即f(i) >= f(j’)=f(i*2-j)
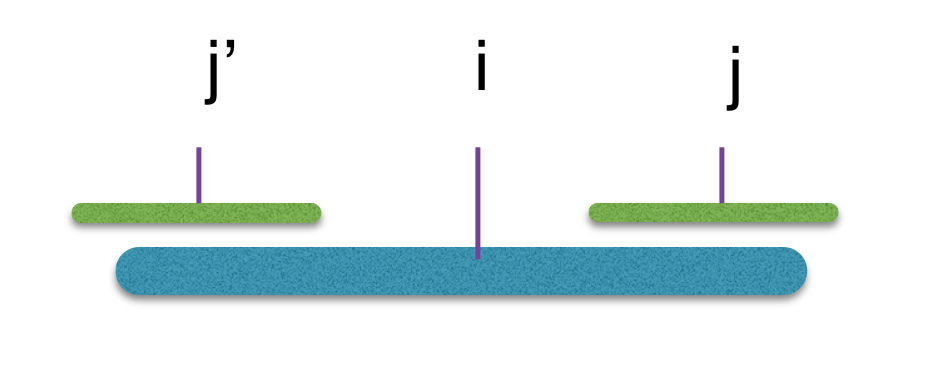
但是还存在上图这样的情况,即i的回文串并没有完全覆盖j’的回文串,那么j与j’的回文串的对应关系就只能在i回文串的范围内才能成立。
那么,这样以来,f(i) >= min(f(j’), f(i)-(i-j)*2)。
有了上述结论,我们可以减少很多的不必要的计算,从而达到高效求解最长回文子串的目的。
题目链接:1032:最长回文子串
思路
Manacher思想,上面已经介绍,但那只能求解最长回文串是奇数的情况,对于偶数来说显然不适用。
其实稍加变通即可。
如:ababa的最长回文串长度为5
而#a#b#a#b#a#的最长回文长度为11。
容易看出,两者是相乘加一的关系
对于任意一个长度为n的字符串,将其穿插于#之间,变为一个长度为2n+1的新串,显然是奇数。
问题迎刃而解了。
代码
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <algorithm>
using namespace std;
char str[1000009];
char t[2000009];
int cnt[1000009];
int manacher(char s[], int len)
{
cnt[0] = cnt[1] = 1;
int id = 1;
int ans = 1;
for(int i=2; i<=len; i++)
{
int num = min(cnt[id*2-i], cnt[id]+id-i);
while(s[i-num] == s[i+num])
num++;
cnt[i] = num;
if(id+cnt[id] < i+num)
id = i;
if(ans < num)
ans = num;
}
return ans-1;
}
int main()
{
int n;
scanf("%d", &n);
while(n--)
{
scanf("%s", str);
t[0] = '$';
int len = strlen(str);
for(int i=0; i<len; i++)
{
t[i*2+2] = str[i];
t[i*2+1] = '#';
}
t[len*2+1] = '#';
t[len*2+2] = '\0';
printf("%d\n", manacher(t, len*2+1));
}
return 0;
}