最小生成树

一个连通图的生成树是一个极小的连通子图，它含有图中全部顶点，但只有n - 1条边，我们把构造连通图的最小代价生成树称为最小生成树。
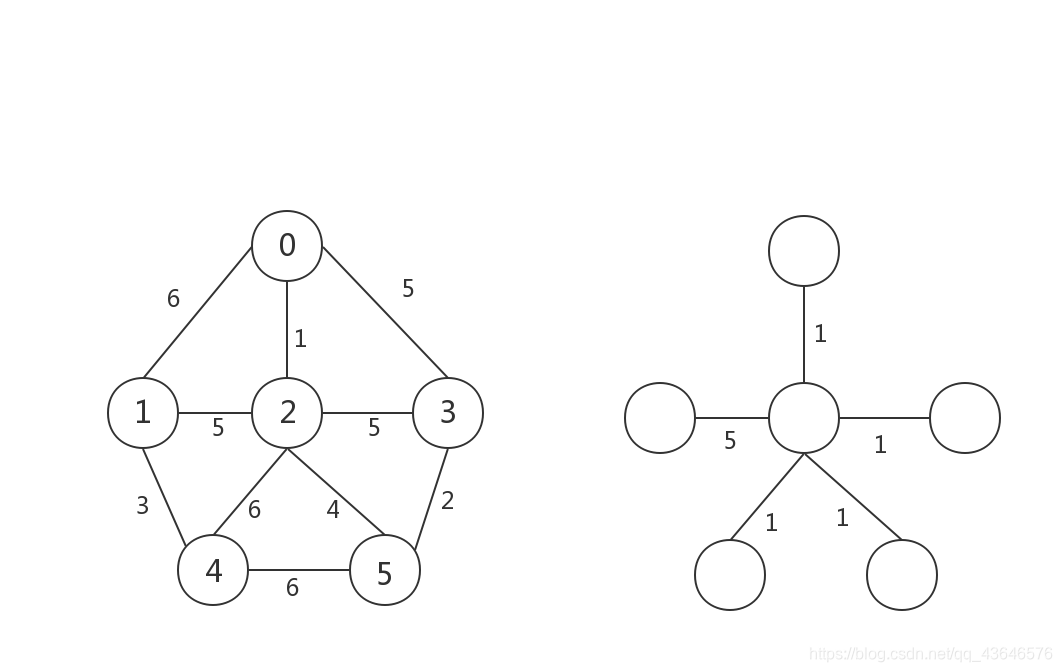
在这里插入图片描述
如上左图所示，这是一个无向带权图，而右图是它的生成树之一。显然，生成树不唯一，可能有多颗。

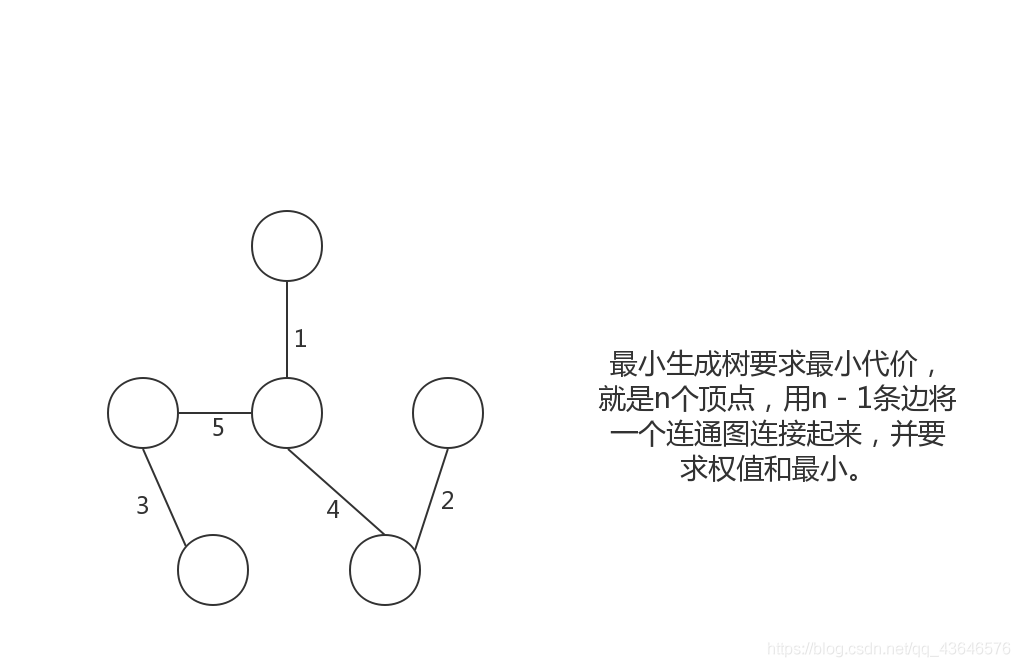
此图才是上左图的最小生成树。

构造最小生成树有多种算法，经典的有两种，Prim算法和Kruskal算法，此篇博客将围绕Kruskal算法展开。

Kruskal算法

Prim 和Kruskal 算法都属于贪心算法，而Kruskal算法的贪心准则是从剩下的边中选择权值最小且不会产生环路的边加入生成树的边集。

基本思想：先构造一个只含 n 个顶点的子图 G，然后从权值最小的边开始，若它的添加不使 G 中产生回路，则在 G 中加入此边，然后按照权值递增的次序依次按规则添加，直至加完 n - 1条边。故，Kruskal算法又称“加边法”。

步骤：

由于Kruskal算法要求按权值由小到大依次添加，所以我们首先要按权值大小排序。
排完序后便要准备开始“加边”了，但“加边”之前要先判断，要加入的这条边是否会使子图形成环。
正式“加边”，合并连通分量。

由于要按权值排序，还要判断是否形成环，所以这里我们定义一个边集数组。

//边集数组
typedef struct
{
   
    int begin;
    int end;
    int weight;
}Edge;

那么上图最后转换后的边集数组为：

	begin	end	weight
Edge[0]	0	2	1
Edge[1]	3	5	2
Edge[2]	1	4	3
Edge[3]	2	5	4
Edge[4]	0	3	5
Edge[5]	1	2	5
Edge[6]	2	3	5
Edge[7]	0	1	6
Edge[8]	2	4	6
Edge[9]	4	5	6

以上图为例，我们来看一下它的最小生成树的生成过程：
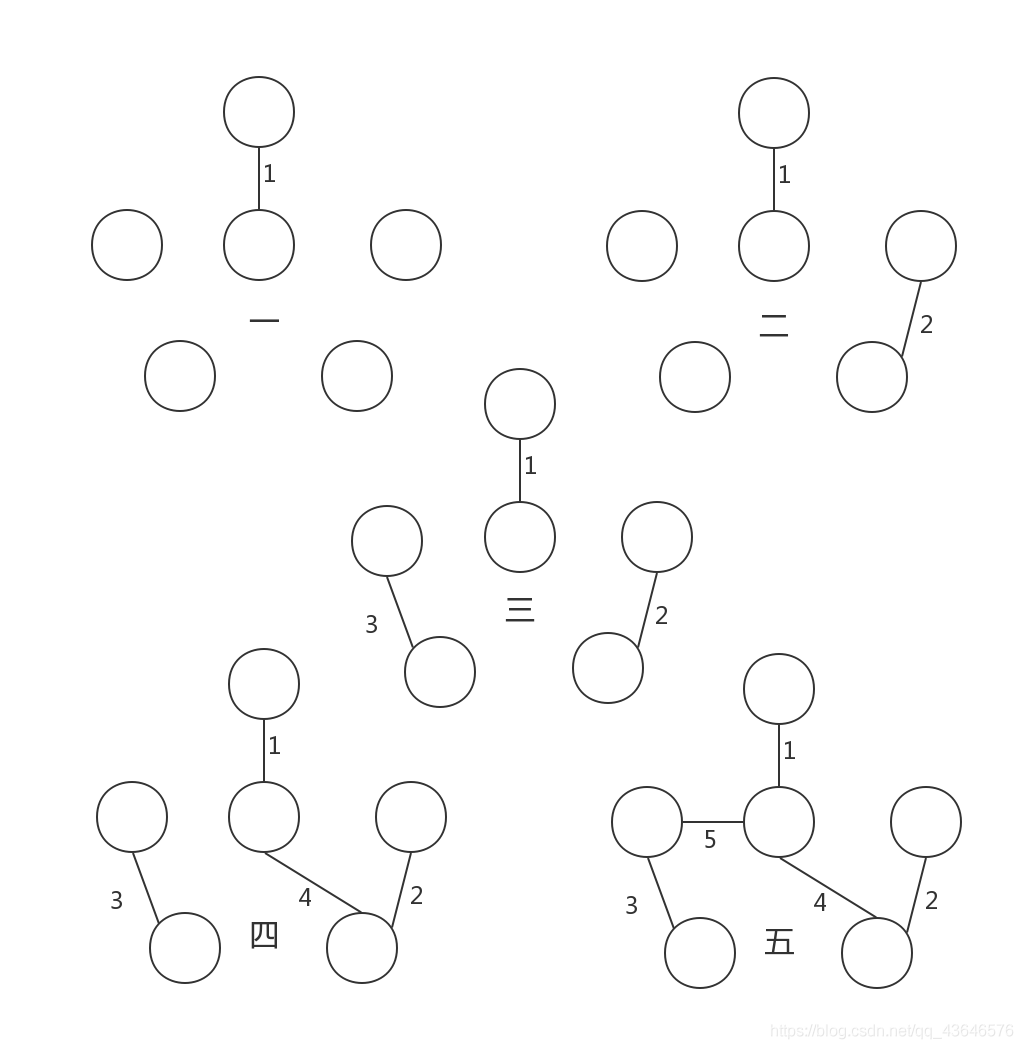
在这里插入图片描述 按照步骤，第五条边应该是（A，D），但由于A，D已在同一集合中，若加边会形成回路，所以（A，D）不加入。

代码

#include <cstdio>
#include <cstdlib>
#include <algorithm>

#define MAXVEX 100      //最大顶点数
#define INF 65535  //极大

typedef struct 
{
   
    int vexs[MAXVEX];           //顶点表
    int arc[MAXVEX][MAXVEX];    //邻接矩阵
    int vex_num, edge_num;      //顶点数，边数
}MGraph;
//边集数组
typedef struct
{
   
    int begin;
    int end;
    int weight;
}Edge;

bool cmp(const Edge& a, const Edge& b)
{
   
    return a.weight < b.weight;
}

//无向图
void CreateMGraph(MGraph *G)
{
   
    int i, j, k ,w;
    printf("输入顶点数和边数：");
    scanf("%d %d", &G->vex_num, &G->edge_num);
    
    //建立顶点表
    printf("输入顶点：");
    for(i = 0; i < G->vex_num; ++i)
        scanf("%d", &G->vexs[i]);

    //建立邻接矩阵
    for(i = 0; i < G->vex_num; ++i)
        for(j = 0; j < G->vex_num; ++j)
            G->arc[i][j] = INF;
    for(k = 0; k < G->edge_num; ++k)
    {
   
        printf("输入边的下标（i , j）及权值：");
        scanf("%d %d %d", &i, &j, &w);
        G->arc[i][j] = G->arc[j][i] = w;    //矩阵对称
    }
}

//查找连线顶点的尾部（该顶点所在连通子图的尾部）下标
int Find(int *parent, int f)
{
   
    while(parent[f] > 0)
        f = parent[f];
    return f;
}

void MiniSpanTree_Kruskal(MGraph G)
{
   
    int i, j, k, n, m;
    Edge edges[G.edge_num];     //定义边集数组
    int parent[G.vex_num];      //判断是否能形成回路
    
    //将邻接矩阵转化为边集数组并按权值大小排序
    k = 0;
    for(i = 0; i < G.vex_num; ++i)
    {
   
        for(j = i + 1; j < G.vex_num; ++j)  //只处理上三角形
        {
   
            if(G.arc[i][j] != INF)
            {
   
                edges[k].begin = i;
                edges[k].end = j;
                edges[k].weight = G.arc[i][j];
                ++k;
            }
        }
    }
    std::sort(edges, edges + G.edge_num, cmp);

    for(i = 0; i < G.vex_num; ++i)
        parent[i] = 0;
    //循环判断每一条边
    printf("最小生成树：\n");
    for(i = 0; i < G.edge_num; ++i)
    {
   
        n = Find(parent, edges[i].begin);
        m = Find(parent, edges[i].end);
        if(n != m)      //没有形成回路
        {
   
            parent[n] = m;      //将此边的结尾顶点加入，表示此顶点已在生成树集合中
            printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight);
        }
    }
}

int main()
{
   
    MGraph G;    
    CreateMGraph(&G);
    MiniSpanTree_Kruskal(G);
    return 0;
}

Kruskal算法的时间代价主要依赖边数，所以对于稀疏图有很大的优势。

参考

《数据结构与算法》——王曙燕
《大话数据结构》