图的遍历——邻接表实现

此篇博客主要就图的储存结构——邻接表展开。

邻接表

图的一种最便于理解的储存结构就是邻接矩阵了（可以简单的把它视为一个二维数组），但是邻接矩阵在处理边数较少，但顶点较多的情况时会浪费不少的储存空间。因此便有了邻接表这种储存结构。

1. 图中顶点用一个一维数组存储， 当然，顶点也可以用单链表来存储，不过数组可以较容易地读取顶点信息，更加方便。另外，对于顶点数组中，每个数据元素还需要存储指向第一个邻接点的指针，以便于查找该顶点的边信息。
2. 图中每个顶点 Vi 的所有邻接点构成一个线性表，由于邻接点的个数不定，所以用单链表存储，无向图称为顶点 Vi 的边表，有向图则称为顶点 Vi 作为弧尾的出边表。

如下图：
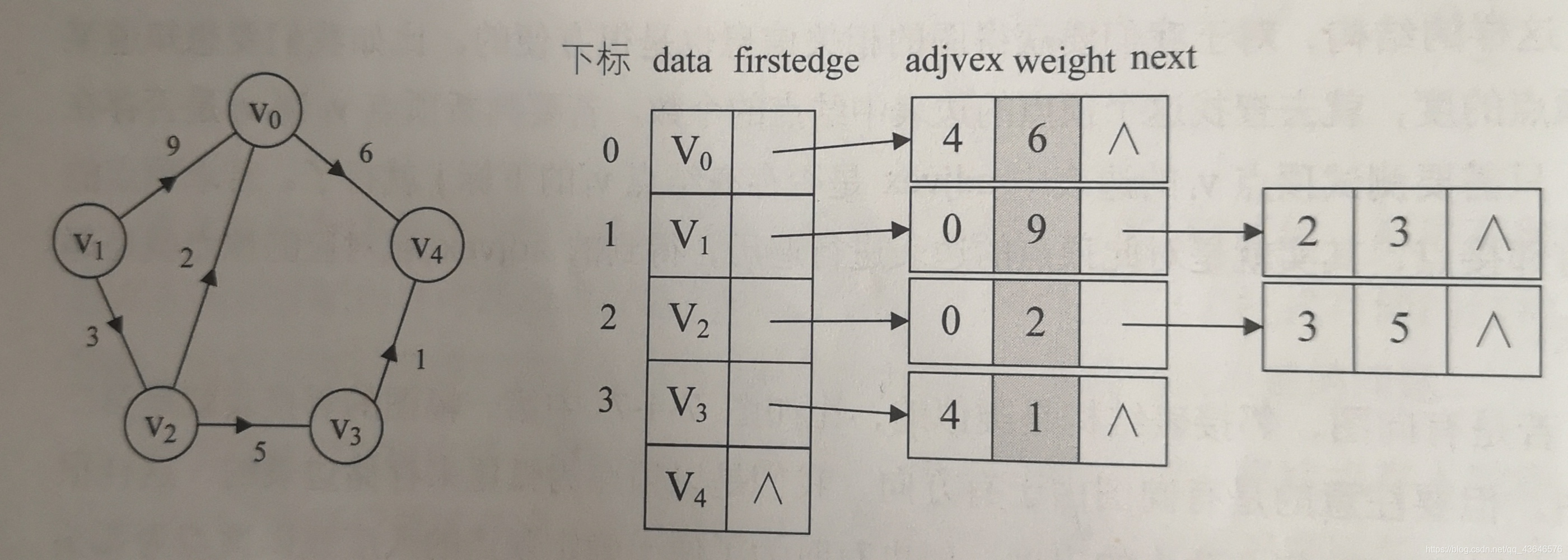根据上图，再来看相关结点的定义就比较好理解了。

//边表结点
typedef struct EdgeNode     
{
   
    int adjvex;             //邻接点域，储存顶点对应的下标
    //int weight;             //权值
    struct  EdgeNode *next; 
}EdgeNode;

//顶点表结点
typedef struct VertexNode
{
   
    int data;               //储存顶点信息
    EdgeNode *firstedge;    //边表头结点
}VertexNode, AdjList[MAXVEX];

typedef struct
{
   
    AdjList adjList;
    int vernum, edgenum;    //当前顶点数，结点数
}Graph;

下来再让我们一起来看一下如何建立邻接表（无向图）。

//建立邻接表
void CreatALGraph(Graph *G)
{
   
    int i, j, k, w;
    EdgeNode *e;
    printf("输入顶点数和边数：");
    scanf("%d %d", &G->vernum, &G->edgenum);

    //建立顶点表
    printf("输入顶点：");
    for(i = 0; i < G->vernum; ++i)
    {
   
        scanf("%d", &G->adjList[i].data);
        G->adjList[i].firstedge = NULL;
    }

    //建立边表
    for(k = 0; k < G->edgenum; ++k)
    {
   
        printf("输入边上的顶点序号：");
        scanf("%d %d", &i, &j);

        //无向图，两次插入（头插法）
        e = (EdgeNode *)malloc(sizeof(EdgeNode));
        e->adjvex = j;
        //e->weight = w;
        e->next = G->adjList[i].firstedge;      //将e指向当前顶点指向的结点
        G->adjList[i].firstedge = e;            //将当前顶点指向e

        e = (EdgeNode *)malloc(sizeof(EdgeNode));
        e->adjvex = i;
        //e->weight = w;
        e->next = G->adjList[j].firstedge;      //将e指向当前顶点指向的结点
        G->adjList[j].firstedge = e;            //将当前顶点指向e
    }
}

图的遍历

从图中某一顶点出发访问图中其余顶点，且使每一个顶点仅能被访问一次，这个过程就叫做图的遍历。

深度优先遍历

简单理解，就是一条路走到黑，不撞南墙不回头???? 。
如下图，给定一个迷宫，要求从顶点 A 出发，访问其余所有顶点。
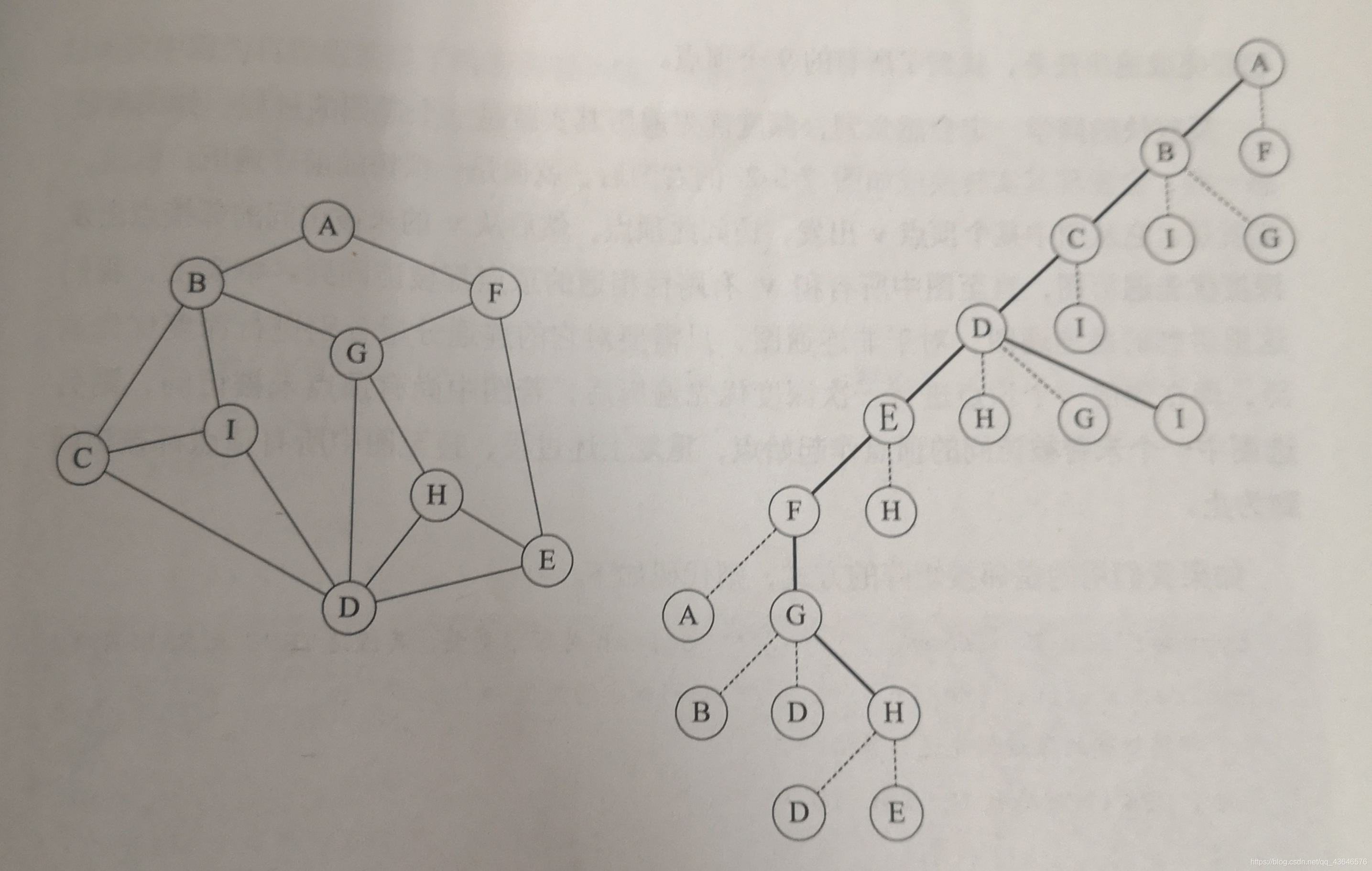加深的黑线便是我们所走过的路程（默认开始走右边的路径），当遇到重复顶点时便会回溯（撞到墙????）。
可以看出，转化为右图后，就相当于一个树的前序遍历。

结论：
从图中某个顶点 V 出发，访问此顶点，然后从 V 的未被访问的邻接点出发深度优先遍历图，直至图中所有和 V 相通的顶点都被访问到。若图中尚有顶点未被访问（非连通图），则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到。

//dfs
void dfs(Graph G, int i)
{
   
    book[i] = 1;
    printf("%d ", G.adjList[i].data);
    EdgeNode *e = G.adjList[i].firstedge;
    while(e)
    {
   
        if(!book[e->adjvex])
            dfs(G, e->adjvex);  //对未访问的邻接顶点递归调用
        e = e->next;
    }
}
void dfsTraverse(Graph G)
{
   
    int i;
    for(i = 0; i < G.vernum; ++i)   
        book[i] = 0;
    for(i = 0; i < G.vernum; ++i)
    {
   
        if(!book[i])    //未被访问
            dfs(G, i);
    }
    printf("\n");
}

上面是dfs的递归版本，再让我们来看一看非递归的吧

//dfs——非递归
void dfs_(Graph G)
{
   
    memset(book, 0, MAXVEX);
    std::stack<int> S;
    S.push(0);
    while(!S.empty())
    {
   
        int n = S.top();
        S.pop();
        if(!book[n])
        {
   
            book[n] = 1;
            printf("%d ", G.adjList[n].data);
        }
        EdgeNode *e = G.adjList[n].firstedge;
        while(e)
        {
   
            if(!book[e->adjvex])
                S.push(e->adjvex);
            e = e->next;
        }
    }
    printf("\n");
}

广度优先遍历

bfs 有一种广撒网的意思????
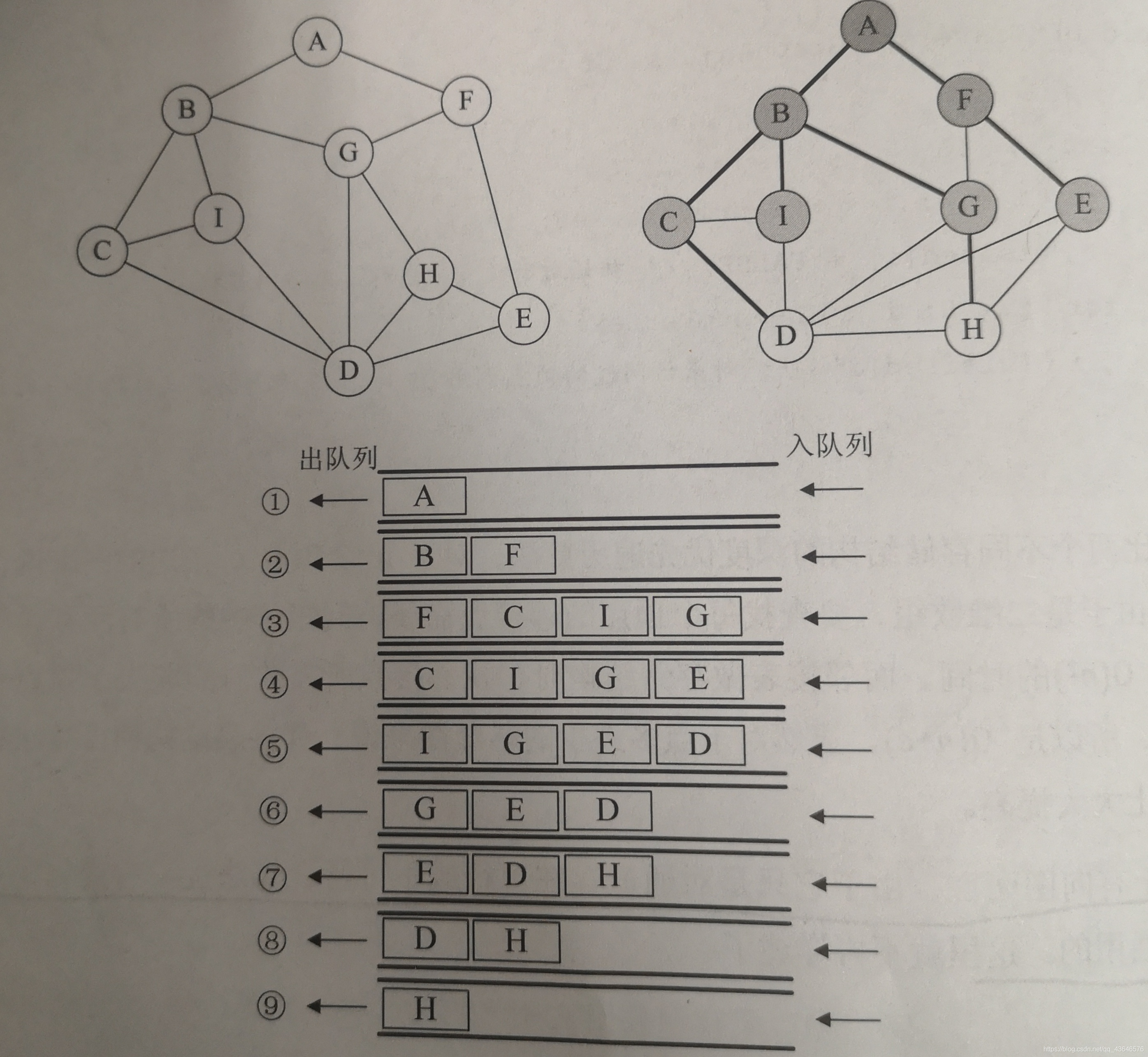dfs 类似于树的前序遍历，而bfs 就有点类似于层序遍历了。

结论：
从图中某个顶点 V 出发，访问此顶点，将与其有边且未被访问的顶点都依次入队，按出队顺序依次执行以上步骤。

//bfs
void bfsTraverse(Graph G)
{
   
    int i;
    EdgeNode *e;
    std::queue<int> Q;
    for(i = 0; i < G.vernum; ++i)
        book[i] = 0;

    for(i = 0; i < G.vernum; ++i)
    {
   
        if(!book[i])    
        {
   
            book[i] = 1;
            printf("%d ", G.adjList[i].data);
            Q.push(i);
            while(!Q.empty())
            {
   
                i = Q.front();
                Q.pop();
                e = G.adjList[i].firstedge;     //当前顶点边表头指针
                while(e)
                {
   
                    if(!book[e->adjvex])
                    {
   
                        book[e->adjvex] = 1;
                        printf("%d ", G.adjList[e->adjvex].data);
                        Q.push(e->adjvex);
                    }
                    e = e->next;    //指向下一邻接点
                }
            }
        }
    }
    printf("\n");
}

补充——销毁边表节点

void DeleteEdge(Graph *G)
{
   
    EdgeNode *e;
    for(int i = 0; i < G->vernum; ++i)
    {
   
        while(G->adjList[i].firstedge != NULL)
        {
   
            e = G->adjList[i].firstedge;
            G->adjList[i].firstedge = e->next;
            free(e);
        }
    }
}

深度优先遍历与广度优先遍历在时间复杂度上是一致的，不同之处在与对顶点的访问顺序不同。
深度优先遍历更适合目标比较明确，以找到目标为目地的情况，而广度优先遍历更适合寻找相对最优解。

参考

《数据结构与算法》——王曙燕
《大话数据结构》